辺の長さがみな等しく、角の大きさもみな等しい形を正多角形という。 The sum of the interior and exterior angles of one angle in a polygon is 180 degrees 多角形の1つの角の内角と外角の和は180°です。 多角形の角のまとめ ・三角形の角の性質 三角形の内角の和は180° 内角外角=180° 三角形の外角はそれと、となり合わない2つの内角の和に等しい ・ n 角形の内角の和 180°×( n − 2 ) ・ 正 n 角形の1つの内角 ( ) 180 ° × ( n − 2 ) n万華鏡の筒に内接する正多角形の一辺を計算で求めたかった。 しかし、角数が増えて計算が大変になってきたので、頼りました。 2 0504 60歳以上 / その他 / 役に立った /
2
多角形の角の大きさ
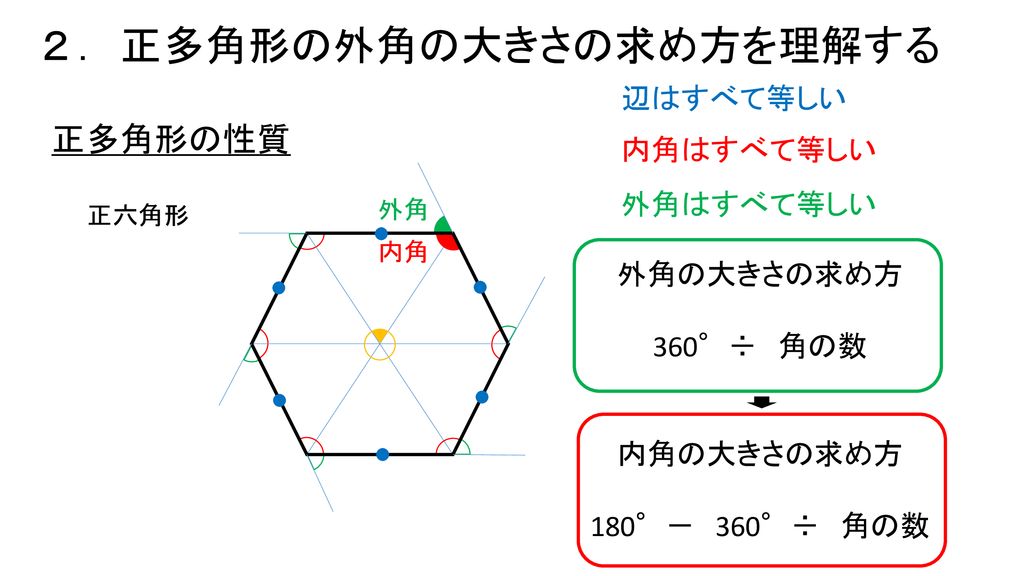
多角形の角の大きさ- この性質は多角形、正多角形に関係なく どんなやつでも全部合わせたら360°になります。 では、このことを使って考えると 正多角形の外角1つ分の大きさは $$\LARGE{360 \div (角の数)}$$ をすることによって求めることができます。 正三角形の場合正多角形のすべての頂点は一つの円周上にある。 つまり正多角形は円に内接する。 最も角の数が少ないのは正三角形である。 三角形では、すべての辺の長さが等しいもの、またはすべての角の大きさが等しいものは必ず正三角形になる。しかし他の多角形では辺の長さがすべて等しく



数学教育 幾何 図形 的見方 多角形
「正多角形」の意味や性質を理解する。 円の中心の周りの角を等分して正多角形をかく方法を理解する。 円の半径の長さを使って正六角形を作図し,正多角形と円の関係について理解を深める。 (本時多角形のある頂点における 内角 とは,その頂点を端点とする 2辺がつくる角の うち 多角形の内部にある方をいう。 すべての内角が 180°よりも小さい多角形を 凸多角形 と呼ぶ。星形多角形 2 星形五角形の角の和を求めよう(∠a+∠b+∠c+∠d+∠e) 下の図のように,多角形の各辺を延長していくと,何回か交わったあと交わらなくなります。 このときにできる図形を星形多角形といいます。星形多角形は1つだけできるとは限り
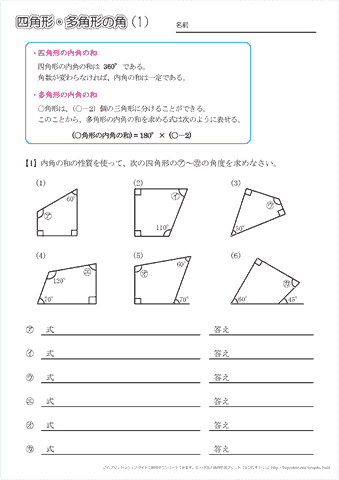
技 未知の四角形の角の大きさを計算で求めることができる。 情報の収集 合同な図形(5年) ・図形の合同について 理解すること 本時4/7 多角形の内角の和(2) ・「多角形」を知り,〇角形の内角の和の求め方を考える 。三角形と角 正 三角形,二等辺 について ・角について 第5学年 c図形 (1) 図形についての観察や構成などの活動を通して,平面図形についての理解を深める。 ア 多角形や正多角形について知ること。四角形・多角形の角(3) 名前 1どんな多角形の角の大きさの和も、いくつかの三角形に分けて求めることができます。 (1)四角形、五角形、六角形は、それぞれいくつの三角形に分けることができるで
・正多角形の性質を,既習の経験を基に辺の長さや角の大きさに着目してとらえようとしている。 算数への関心・意欲・態度 (2) ・三角形の内角の和が180°になることを,敷き詰める活動などを通し三角形の内角の和や外角を利用して,いろいろな角の和を求めてみよう。 多角形の内部に入り組んだ図形の角の和 2 多角形の内角の和の利用 (1)~(3)の図形の角の和を求めよう。 ∠x を ∠a,∠b,∠c で表してみよう。(3つの角を1つに集めよう。 多角形の角などの詳細を設定するためには「変形パネル」内で調整することが出来ます。 この変形パネル内での詳細設定は四角形や楕円でも使用出来ますので色々試してみてください。 まとめ いかがでしたか?



小5 算数 小5 33 多角形の角 Youtube



内角の大きさが150度である正多角形 出石で数学をがんばりたい
図1のように、多角形の1つの辺とこれに隣接する辺の延長とがなす角を外角という 外角は内角の補角である (内角)(外角) =180° (外角) =180°− (内角)2.多角形の角 三角形の3つの内角の和が180°であることの証明 abc の辺bc を延長した直線をbcd とし, 点c を通り辺ba に平行な直線をce とする。 ba//ce より 平行線の同位角は等しいので,∠b =∠ecd ②( ) ①,②より ∠acb +∠a +∠b =∠acb +∠ace +∠ecd 正多角形の内角を4秒で計算できる公式 正多角形の内角を計算したいんだけど?? こんにちは!この記事をかいているKenだよ。映画は1日2本までだね。 正多角形の内角 を知りたいときってあるよね?? 多角形の内角の和は公式つかえばドヤ顔できるけど、



多角形の内角と外角 思考力を鍛える数学




多角形の角度の和の求め方 添付画像の黒い印の角の角度の和を求めたいのです Okwave
1) 頂角の和が180度になる星形多角形を調べよう。 2) 星形偶数多角形の性質を調べよう。 ・星形五角形の頂角の和を求めるときに使った, の考え方がよく使われていることに気づいた生徒は数人。 <生徒のレポート例>38 多角形の角(2) 章 制限時間 合格点 4 30分 80点 点 多角形の内角の和は、三角形の数×180° で求めることが出来ます。 1つの頂点から対角線をひいて、いくつの三角形に分けられるかを考えます。どうも秋山です。 今日は中華料理をたらふく食べたので満足です! では、mayaの学習を始めましょう! 多角形ポリゴン 一般的には、3角形や4角形も多角形といいますが、3dcgでは、5つ以上のバーテックスで成り立っているポリゴンを多角形ポリゴンと言います。




多角形の内角の和 一覧表と簡単公式による求め方 Yattoke 小 中学生の学習サイト




多角形の内角の和 算数の公式覚えてますか
凸多角形の定義と認識方法 点列P=(p 0, p 1, p 2, , p n=p 0)が凸多角形を成すかどうかの判定: s ij 頂点p iとpjを結ぶ線分(対角線),ij≧2 仮定:多角形の辺は反時計回り(内部は辺の左)に順序付角 とができる。 形 ・三角形の内角、外角の性質を用いて、必要な角の大きさを求 の めることができる。〔ワークシート〕 角 5 多角形の内角の和 ・多角形の内角の和を予想し、それが正しいことを既習事項に 帰着させて考えようとしている。 多角形(四角形・五角形・六角形・・・)の内角の和の公式&問題の解き方 管理人 10月 6, 18 / 11月 18, 18 そしてその中でもさらに多角形の内角の角度に関する問題は頻出されま




無料 中2数学 標準問題 解答プリント 223 図形3 多角形の角



2 47 第3章多角形の角 多角形の外角の和
角の和 1 1 つ 1 1 つの角の大きさではなく、いくつかの角の和を求めよという問題 があります。 1 1 つ 1 1 つの角の大きさは求まらないことが多く、 角を集めていくことで解決します。 角を集めるためには、三角形の外角を用います。 中2数学。「角と平行線」の次は「多角形の角」。多角形の角 内角(ないかく):図形の内側にできる角 外角(がいかく):図形の外側にできる角 「図形の外側」とは、1つの内角に注目した時、その内角に触れている一辺を延長した際にできるスペースです。 簡単に言えば、内角のとなりに 多角形の内角の和、外角を利用した問題です。基本公式をしっかり理解して解いていきましょう。 基本公式 *多角形の外角の和は360°になる 公式を丸暗記するのではなく、公式の導き方を教科書で確認し、自分でも証明できるようにしておいてください。




多角形の内角の和 は何度なのか を説明します おかわりドリル
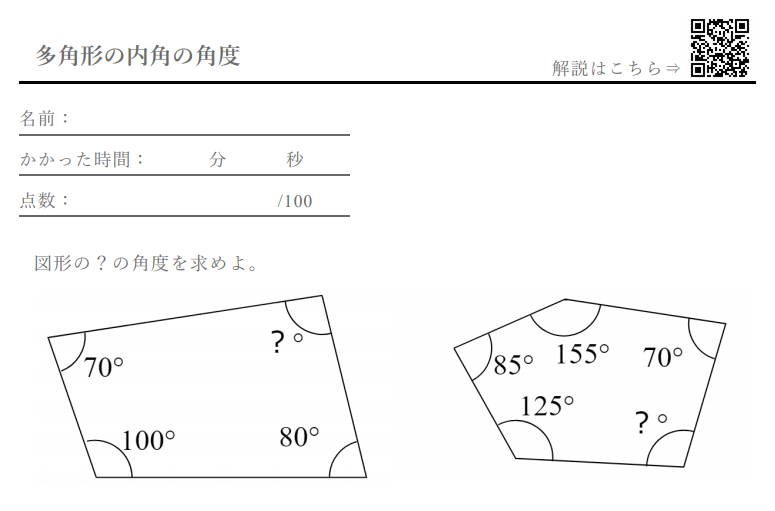



多角形 の内角の角度 計算ドリル 問題集 数学fun
これを31で示した多角形tに置き換えて考えてみましょう。 つまり、点pと多角形tの単位円 上に点qを設置し、点pと頂点 からなる線分 と点pと頂点 からなる線分 がなす で を考えます。 の場合、 点qを反時計回りに通過しているので、 は1されます。 の場合、 角 下の図のように、2つの半直線 OA, OB によってできる図形を、角(angle) といいます。 ちなみに、半直線とは、基本点と直線で見たように、片方の点から出発してもう片方の点のほうへ伸びていく線のことを言います。 角に対して、2つの半直線の共有点を、角の頂点といいます。1 単元 「図形の角を調べよう」(東京書籍 5年) 2 単元の目標 三角形や四角形の内角の和について理解し、それを用いて多角形の角の性質を考える力を養う とともに、帰納的及び演繹的に考えるよさに気付き、今後の生活の学習に活用しようとする態度
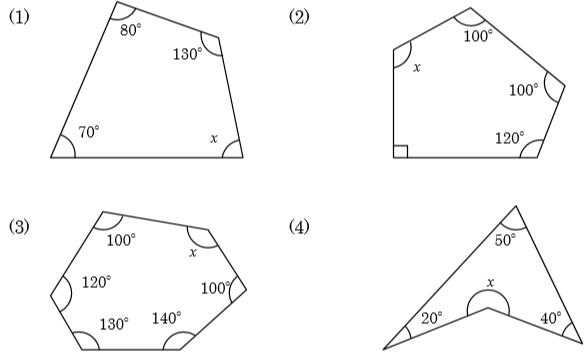



中2数学 多角形の内角の和と外角の和のポイントと練習問題 Pikuu




内角の和 180 N 2 外角の和 360 教遊者




内角の和が1260度である正多角形の外角の大きさの求め方を教えてください Clear




等角連続整数辺多角形は存在するのか 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog
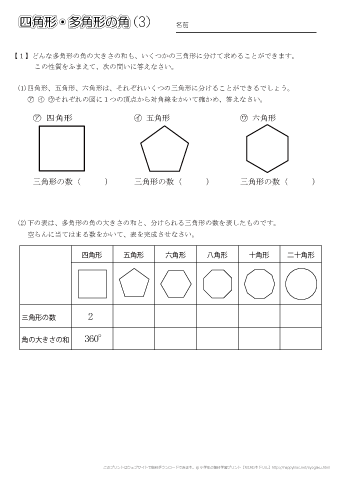



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生




多角形の角 無料で使える中学学習プリント
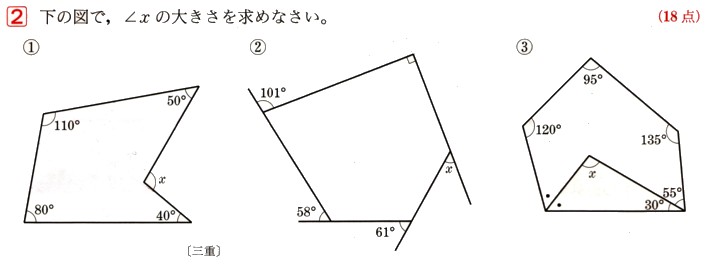



中学2年数学 図形の調べ方 三角形 多角形と角 確認問題2 解答 あんのん塾




4 9 Atimes2 Descubre Como Resolverlo En Qanda
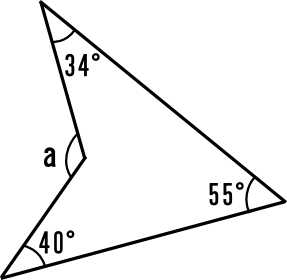



中学2年数学練習問題 図形の調べ方 多角形の内角と外角の解答
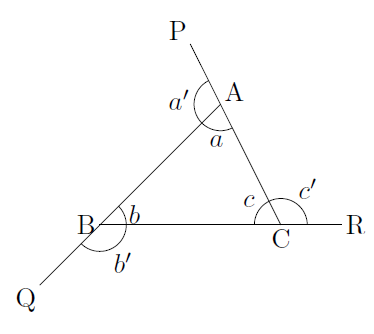



多角形の外角の和 まなびの学園
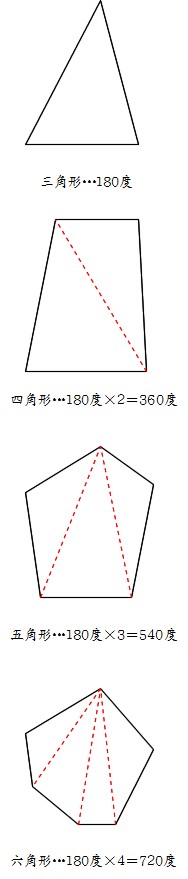



Math 多角形の内角の和 働きアリ



正n角形の内角の和は2 n 2 直角である 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学
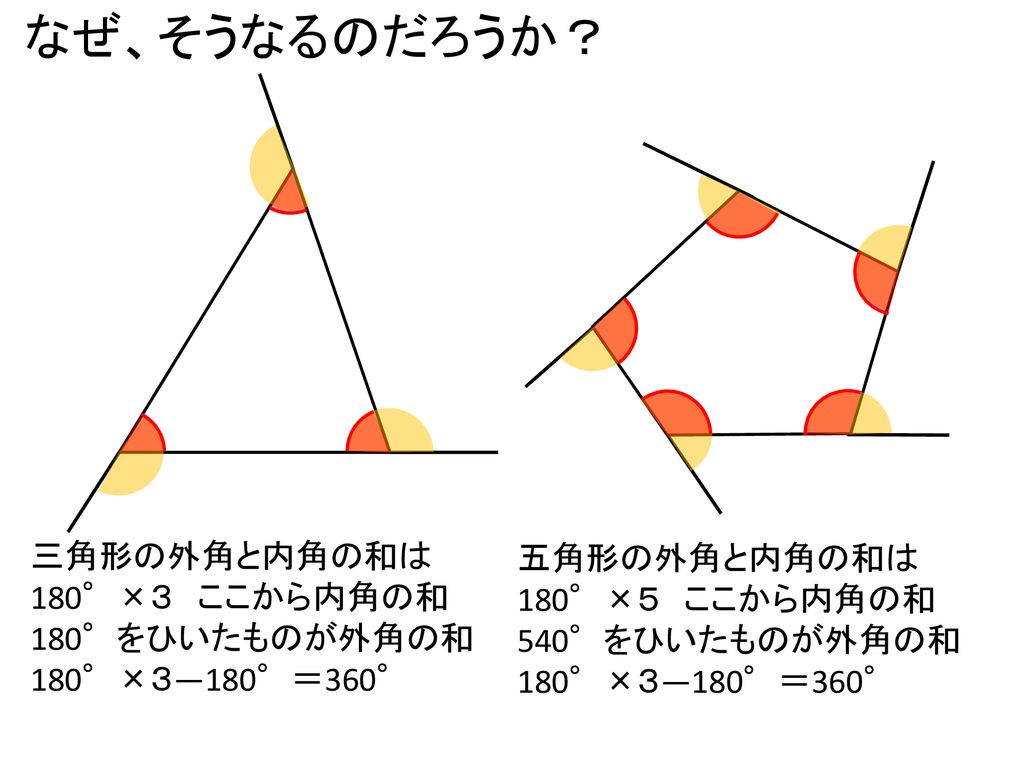



多角形の外角の和 凹型四角形の角 星形五角形の内角の和 Ppt Download



2




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく
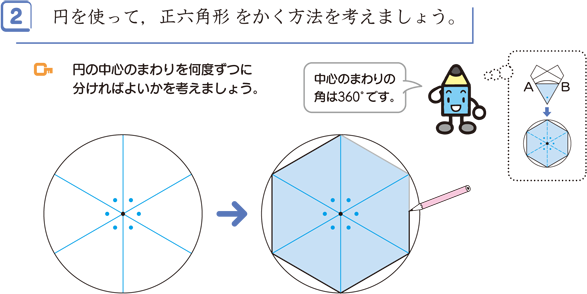



正多角形 算数用語集
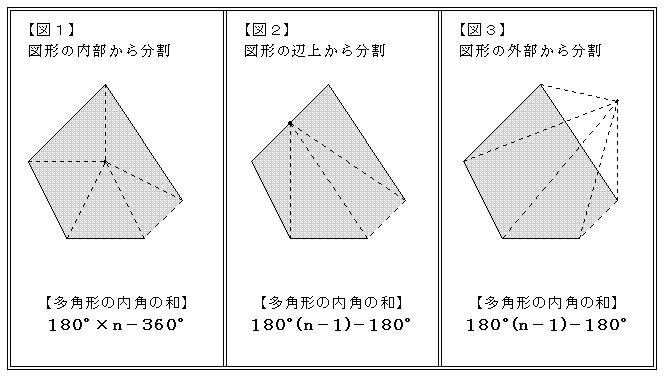



多角形の角
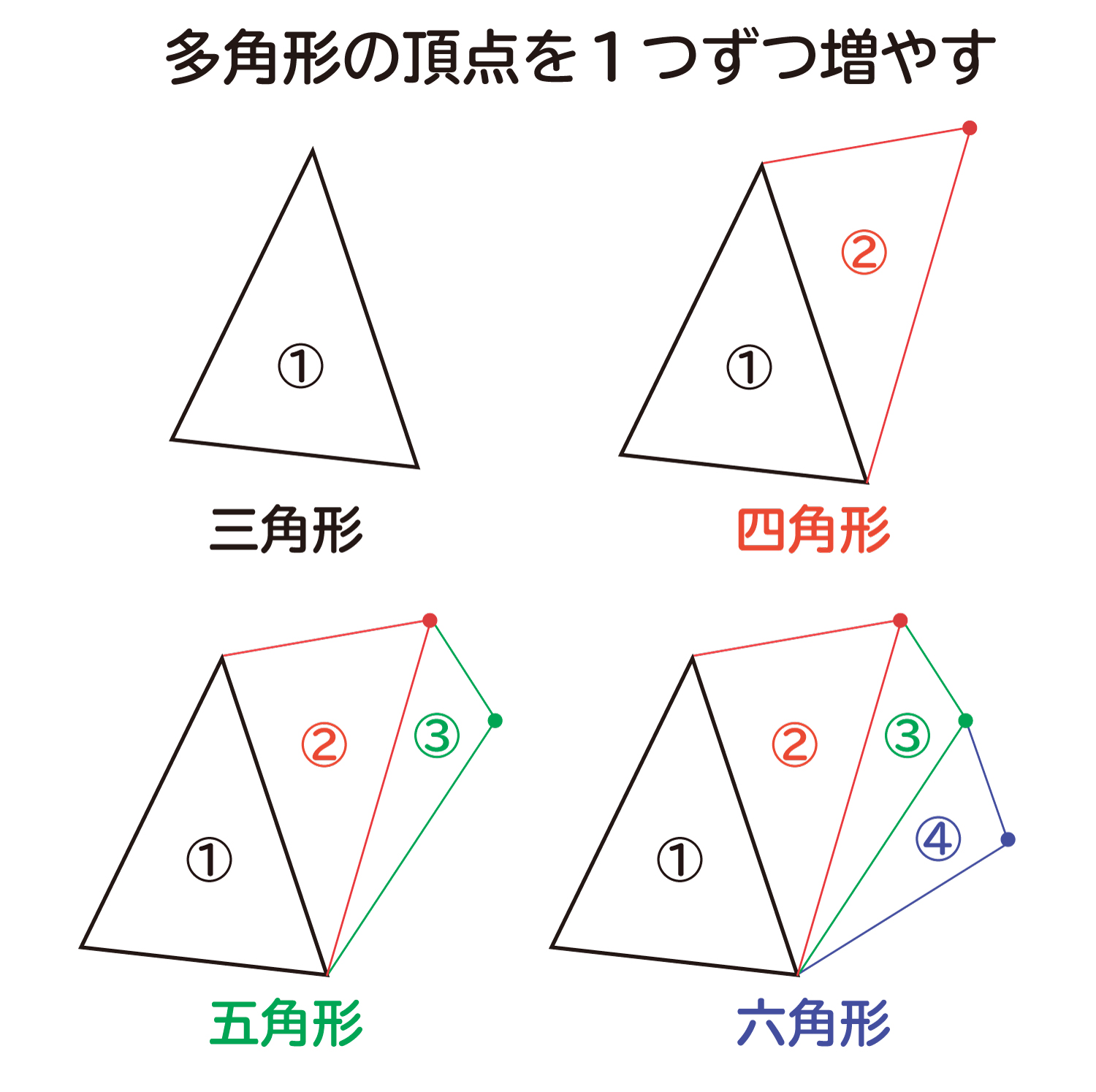



なぜ n角形の内角の和は 180 n 2 なのか を説明します おかわりドリル




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




数学 中2 51 多角形の内角と外角の和 基本編 Youtube
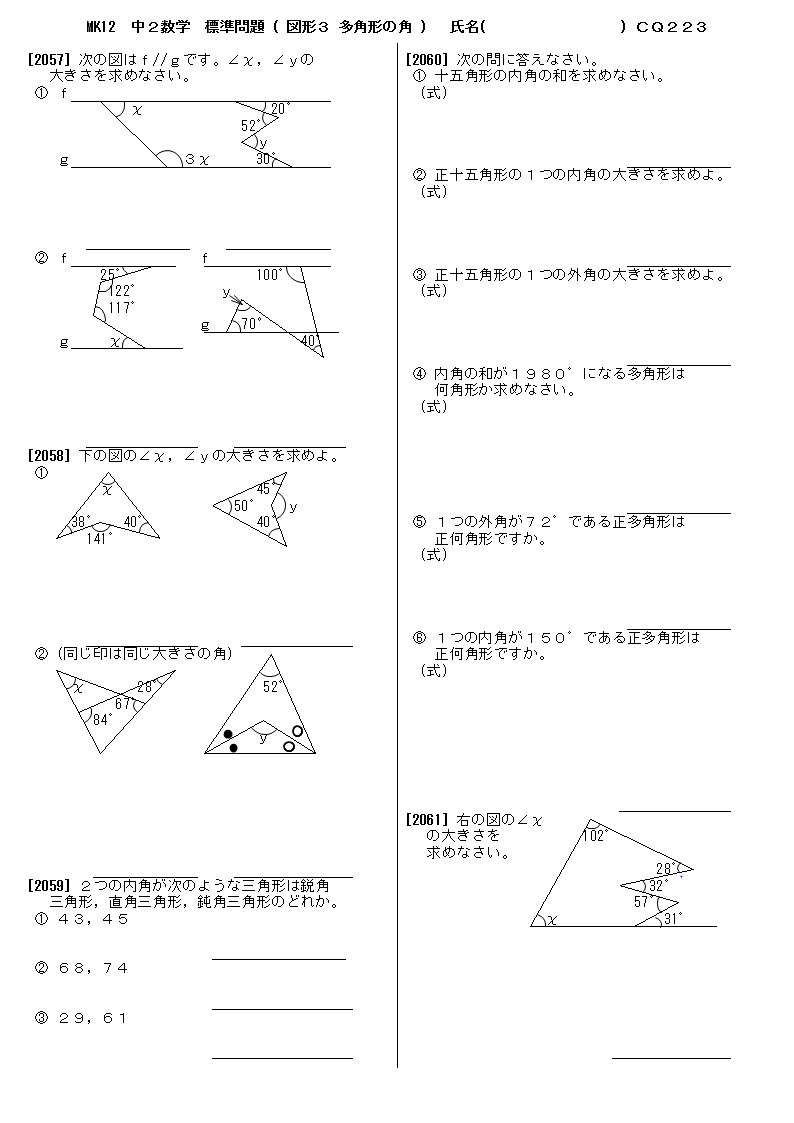



無料 中2数学 標準問題 問題プリント 223 図形3 多角形の角




多角形の内角の和 外角の和の公式 数学fun



多角形の内角と外角 思考力を鍛える数学



1
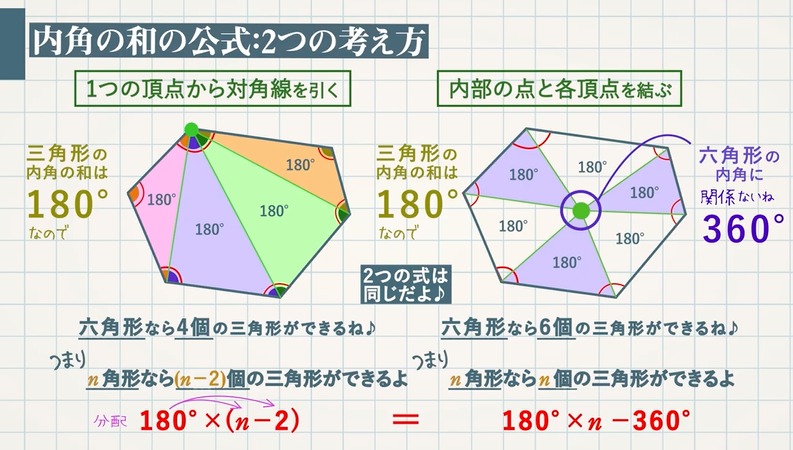



内角の和 180 N 2 外角の和 360 教遊者



2 48 第3章 多角形の角 いろいろな図形の角 プログラミングの雫



1



正多角形の内角と中心角 家紋の描き方007b 夏貸文庫




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト



正多角形の1つの内角 外角を求める方法を問題解説 数スタ
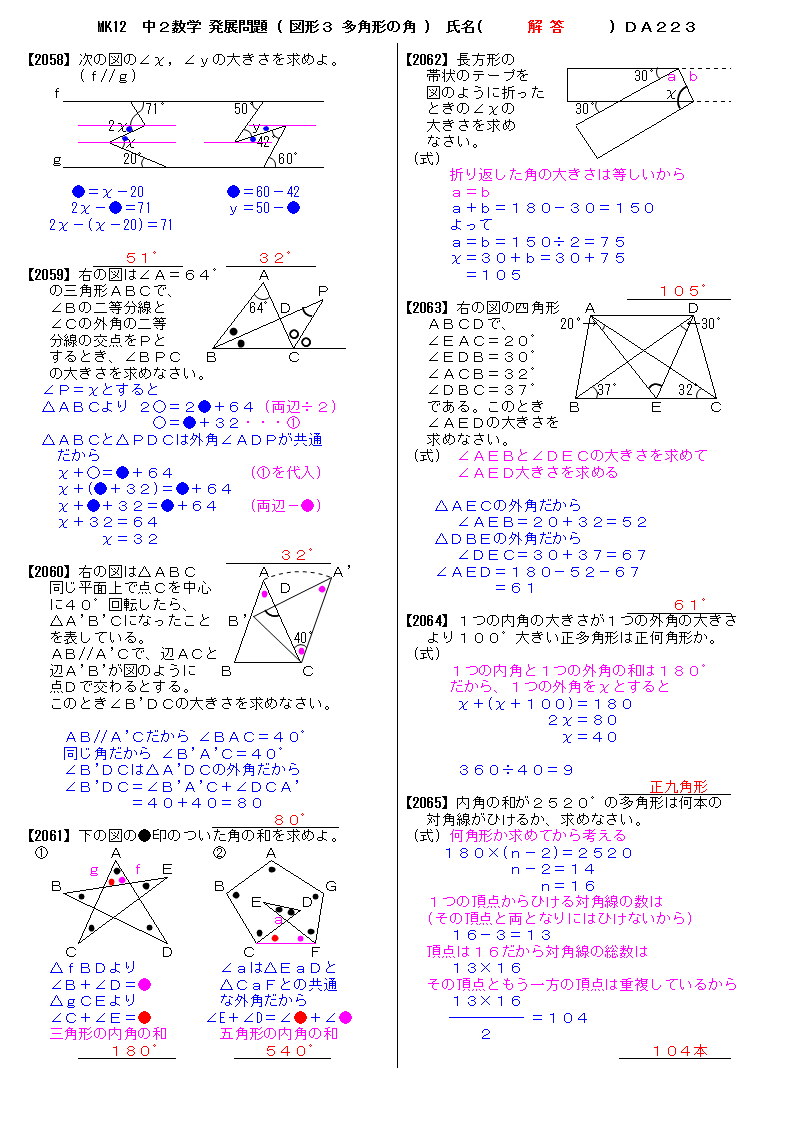



無料 中2数学 発展問題 解答プリント 223 図形3 多角形の角




図形 角度 錯角 同位角 多角形の内角外角など 現役塾講師のわかりやすい中学数学の解き方
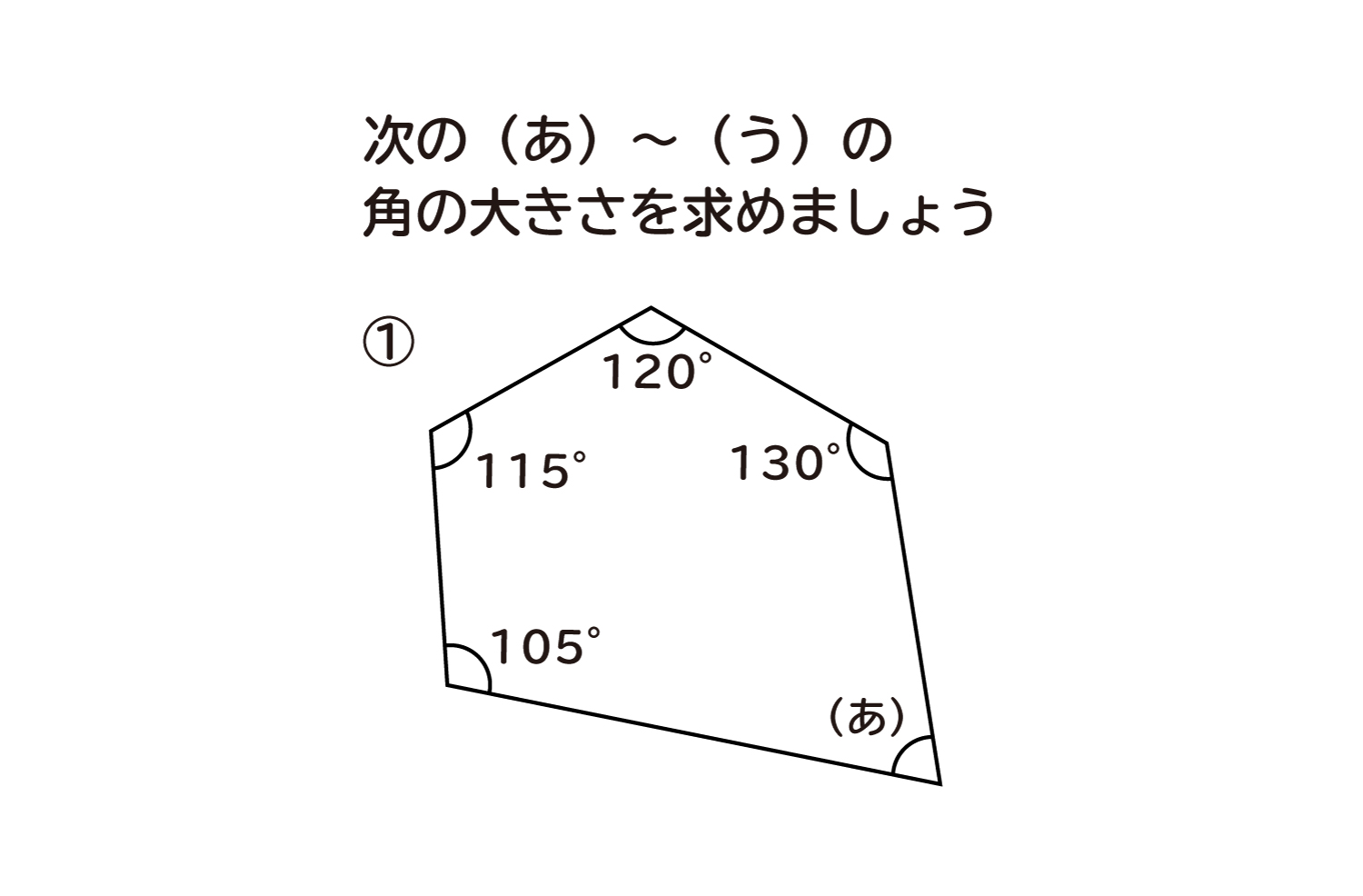



小学5年生 算数 無料問題集 多角形の角の大きさ おかわりドリル




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学




Cdn Clearnotebooks Com Uploads Page File



1
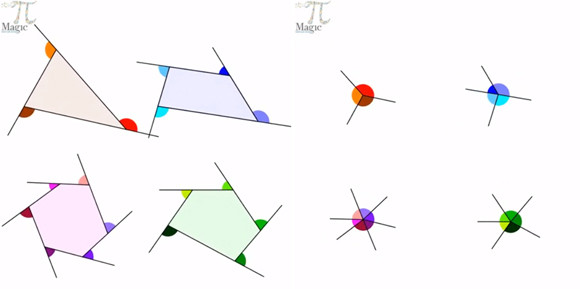



多角形の外角の和は360度 をgifアニメで表現 これがわかりやすいと海外で話題に カラパイア




多角形の内角の和 は何度なのか を説明します おかわりドリル
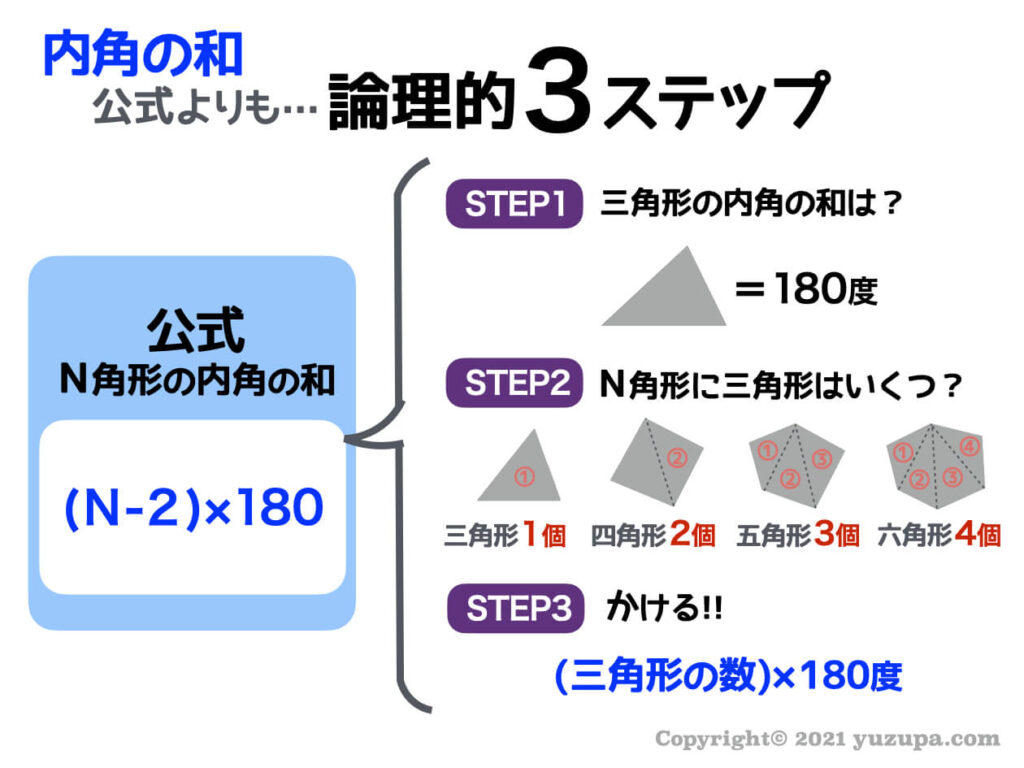



中学受験 多角形の内角の和 公式を忘れなくする論理的3ステップ かるび勉強部屋
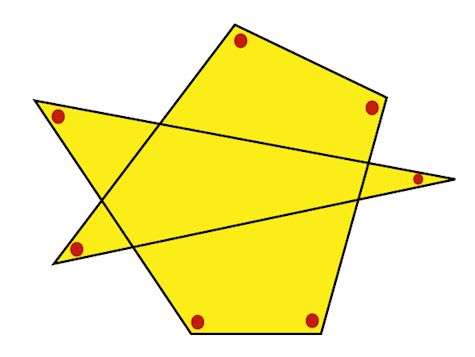



変形多角形の 内角 名寄 算数数学教室より
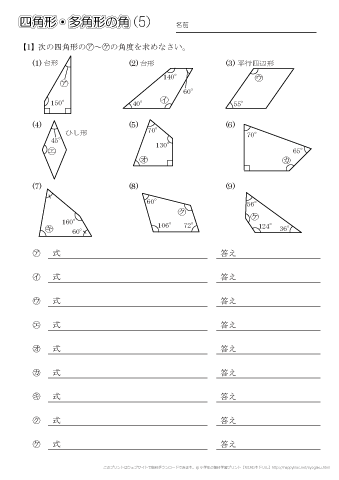



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生
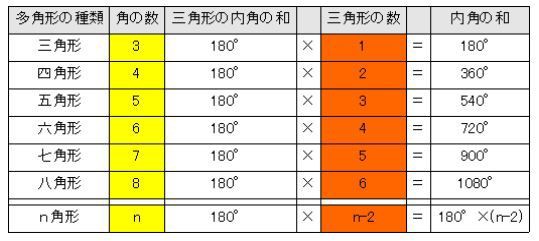



内角攻め それとも外角攻め すうがくラボのブログ



多角形の内角の和を簡単に求める方法 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ



多角形の内角と外角 思考力を鍛える数学




中2数学 複雑な多角形 角の和 応用問題



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生



正多角形の作図 プログラミングで多角形を描く方法を考えよう 1時間目 Ppt Download



数学教育 幾何 図形 的見方 多角形




多角形の内角と外角 の問題のわからないを5分で解決 映像授業のtry It トライイット



Studydoctor多角形の角度の問題 中2数学 Studydoctor



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生




内角の和の公式 内角の和が1800 の多角形は何角形 中学や高校の数学の計算問題



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
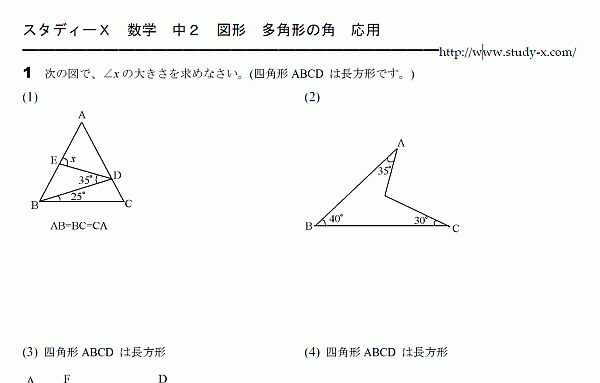



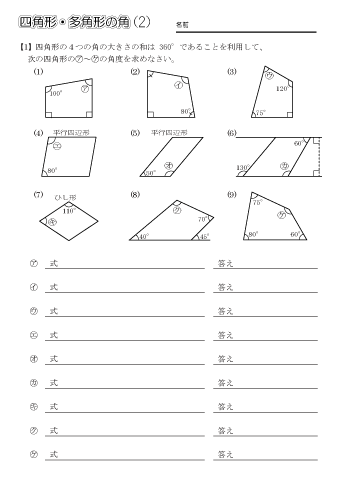
多角形の角 応用 無料学習プリント教材




多角形の内角と外角 の問題のわからないを5分で解決 映像授業のtry It トライイット
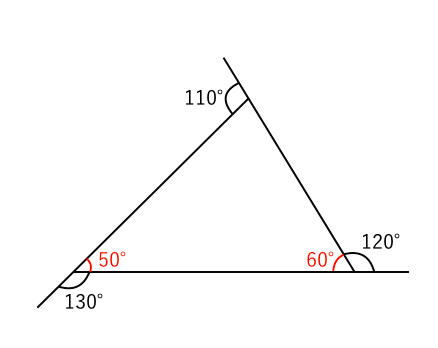



図形の調べ方 外角を求める 苦手な数学を簡単に




n角形の内角の和 中2 多角形の内角と外角 数楽者のボヤキ ツブヤキ ササヤキ 中学 数学 道徳 Mathematics Puzzles




板さんの短時間学習クリニック 一枚 中学数学 高校入試数学問題各単元解説




中2数学 複雑な多角形 角の和 応用問題



2




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学



正8角形です あ い う それぞれの角度の求め方を教えてください 一つの角の Yahoo 知恵袋




中学2年生 多角形の内角外角 公式 個別進学教室マナラボ受験 教育情報サイト




多角形の角 図で Xの大きさを求めてください 解き方の説明もあればうれ Okwave
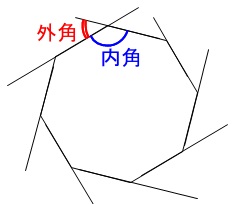



多角形の内角の和の公式と外角の和を利用した角度の求め方
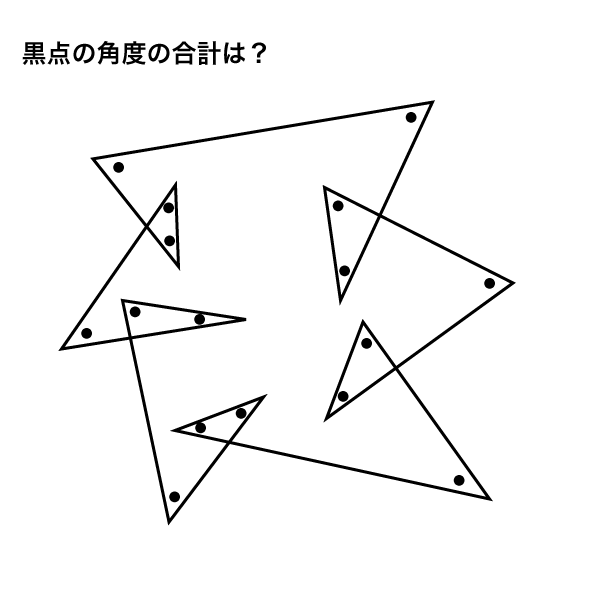



角度情報がない図形の合計の角度 星形多角形 受験算数入門



角と平行と多角形 わかる数学




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
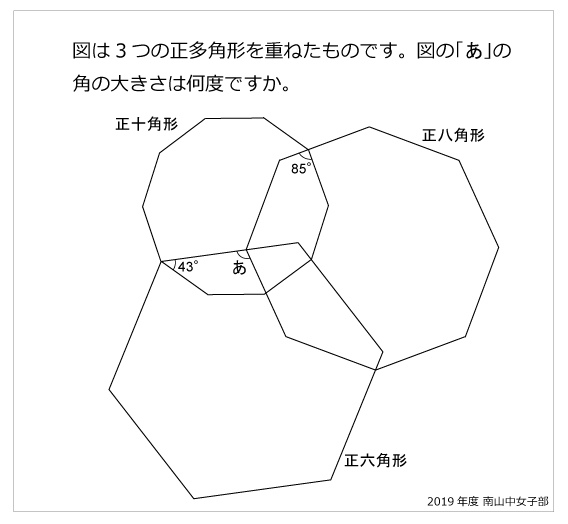



今年の1問 19年南山中女子部 正多角形と角 算数星人のweb問題集 中学受験算数の問題に挑戦



Www Tsumugi Ne Jp Member Data Sm2 4 Sm2 4 3 Pdf




小学校5年 算数 正多角形の角の大きさ Youtube
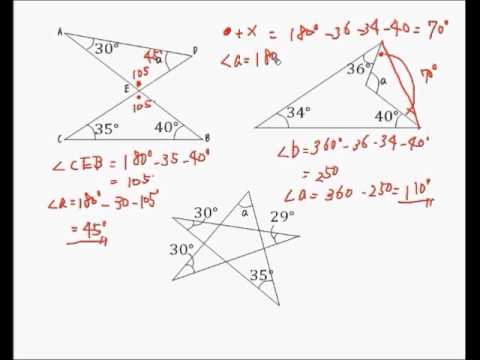



多角形から角を求める Youtube



1



2




中学2年生 多角形の内角外角 公式 個別進学教室マナラボ受験 教育情報サイト




内角の和 180 N 2 外角の和 360 教遊者
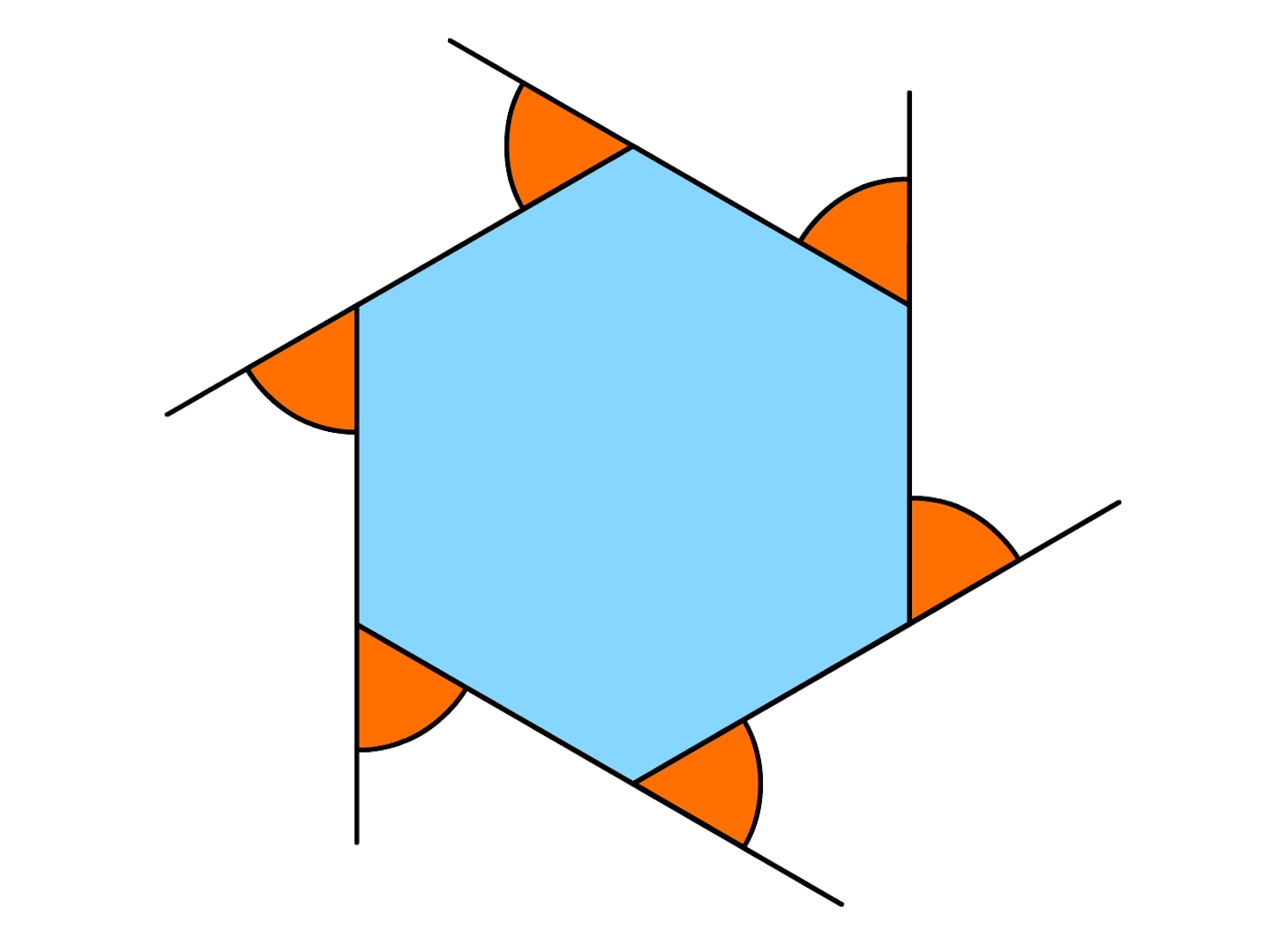



2年 多角形の外角 数学イメージ動画集 大日本図書




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく




内角の和 算数用語集
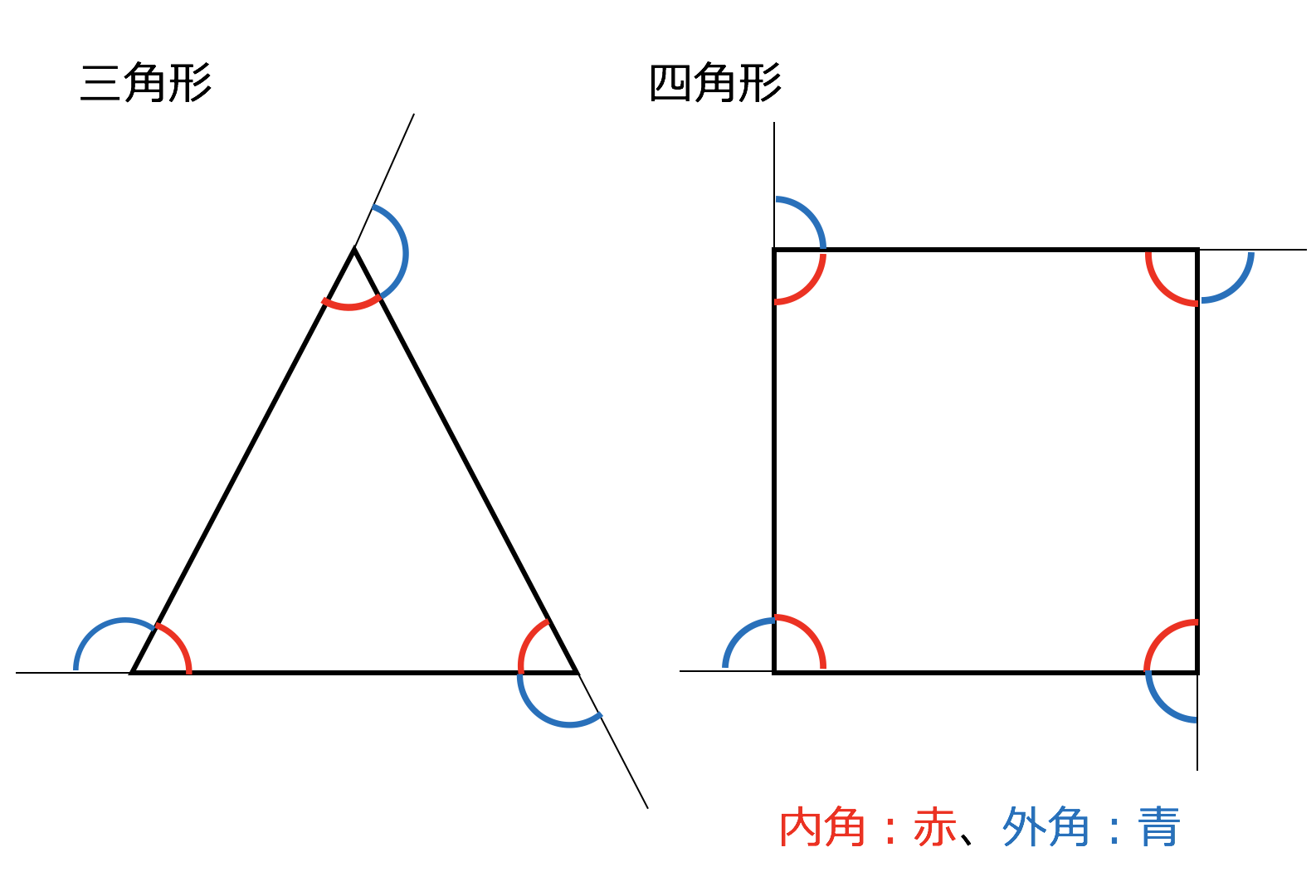



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ
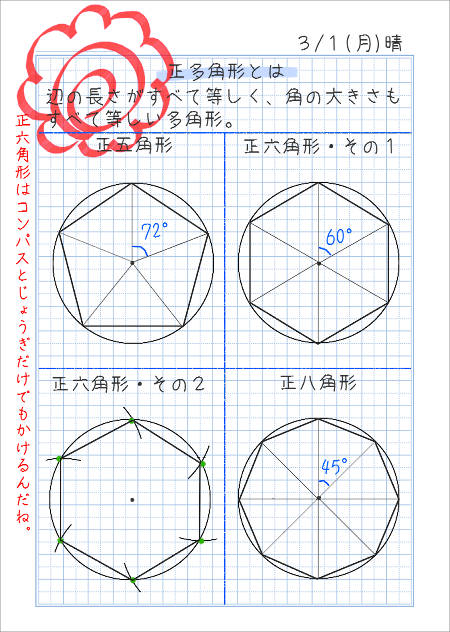



いろいろな正多角形をかいてみよう 家庭学習レシピ




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく
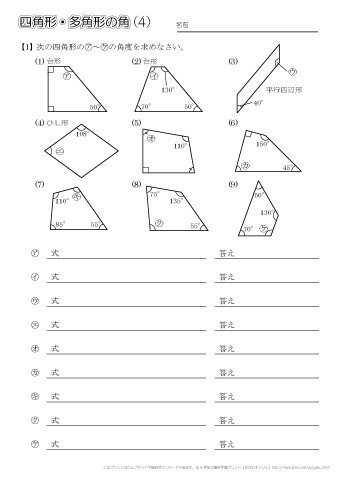



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生
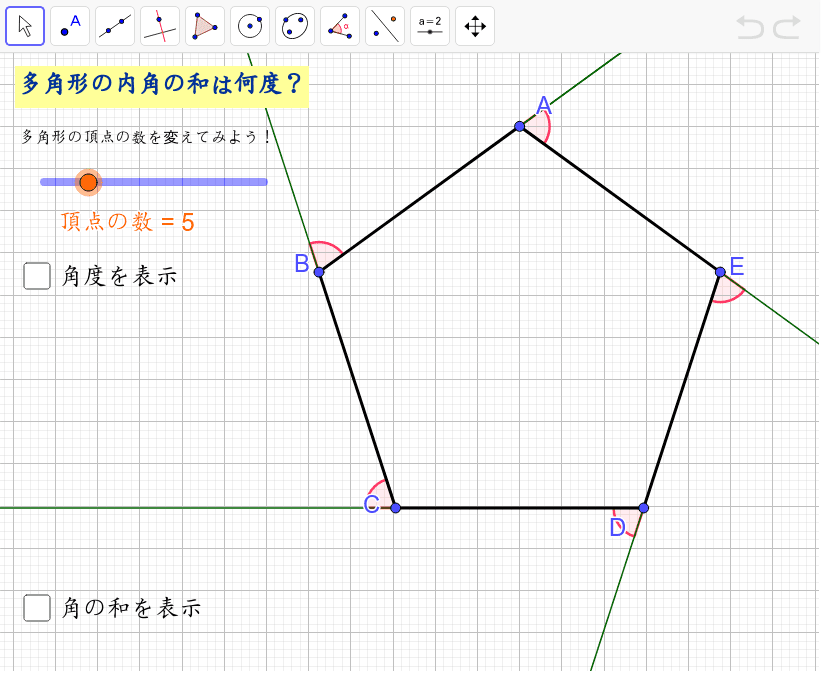



多角形の外角 Geogebra
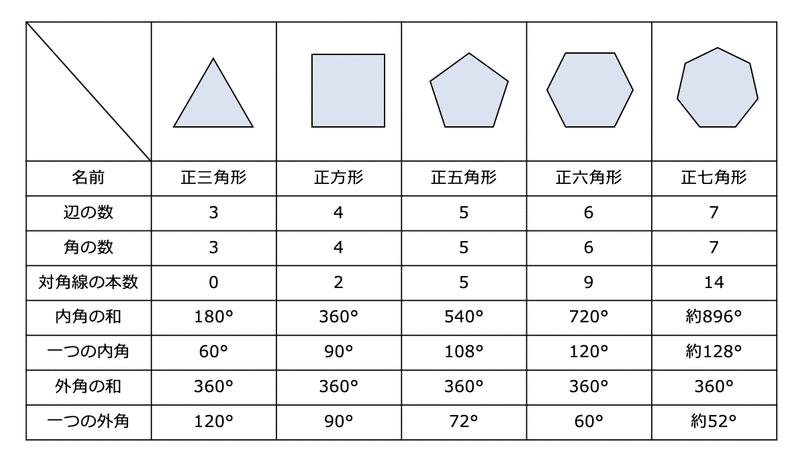



実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note




Descubre Como Resolverlo En Qanda




正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より
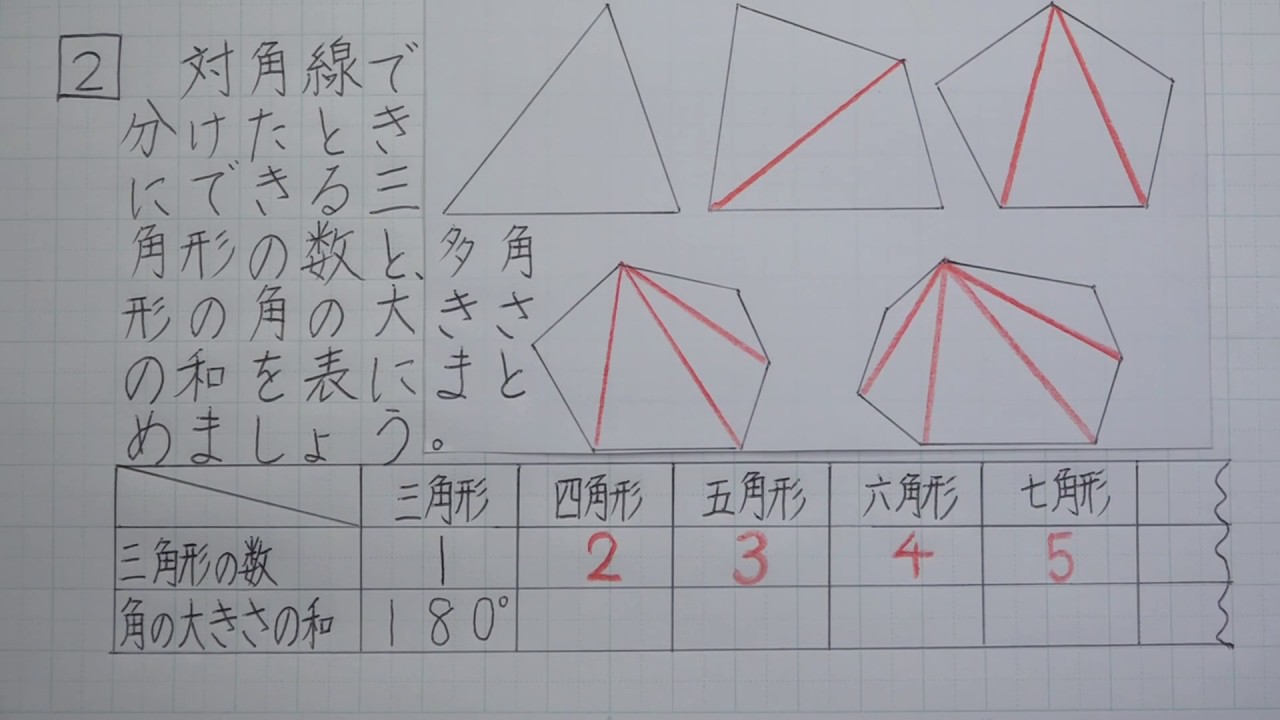



旧バージョン 5年算数 図形の角と合同 8 多角形の角の大きさの和を調べよう Youtube



正多角形の角数を大きく増加して行くとその内角は180度に近づく 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく



中2数学多角形の角こちらの問題を考えてほしいです X 85 Yahoo 知恵袋
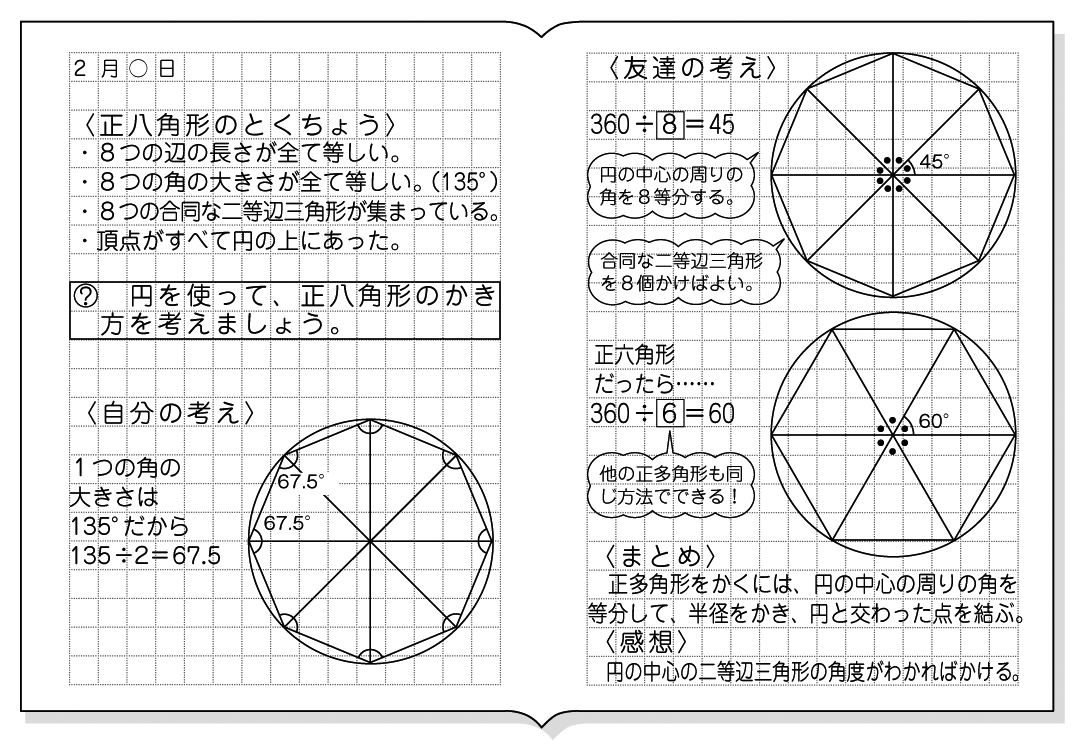



小5算数 正多角形と円 指導アイデア みんなの教育技術



0 件のコメント:
コメントを投稿