数学24章図形の調べ方「図形の合同」<応用問題> 組 番 名前 AさんとBさんが,次の要素で三角形をかきましたが,二人がかいた三角形は,合同にはなりま せんでした。次の問いに答えなさい。2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ② 2 下のように「平行四辺形の2組の向かい合う辺はそれぞれ等しい」ことを証明しました。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru

中2数学 二等辺三角形の証明 例題編 映像授業のtry It トライイット
合同の証明 応用
合同の証明 応用-22 第6 章 合同式の応用,剰余類 とくに,a が9 で割り切れるためにはD (a) = 0 が必要十分である.10 1 (mod 3) より,上の議論は3 の倍数の判定にも使える.すなわち,a の各桁を(3;6;9 が現れた ら0 とみなして) 足すことを一桁の数になるまで繰り返し,その結果をD 0(a) とすれば,角, 円, 外接円, 合同, 作図, 幾何, 中線, 平行四辺形, ひし形, 回転, 正方形, 三角形 中学生でも解ける、大学生でも解けない難問。 ジオジェブラの作図機能を使って考えてみよう。 ジオジェブラは正確なので、図に頼らないで、なぜそのことが言えるのかを



中学数学 証明 二等辺三角形であることの証明 中学数学の無料オンライン学習サイトchu Su
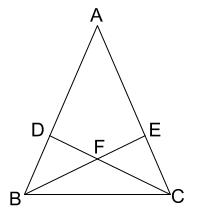
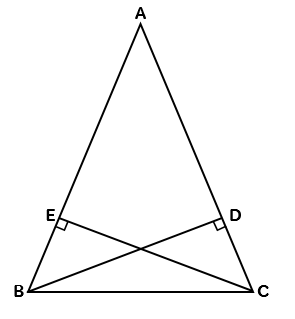
合同式を等式に変換すると容易に証明できる \\1zh ac\equiv bdにおいてcをa,\ dをbにすると\ \ a^2\equiv b^2 これを繰り返すと\ \ a^n\equiv b^n \\\\ よりわかりやすいように,\ 具体例も示しておく \\2zh a,\ bをそれぞれ5で割ると1,\ 3余る数とすると,\ a=5q_1\underline{1},\ \ b合同証明3 pcが線分abの垂直二等分線のとき apc≡ bpcとなることを証明しなさい。 a b c p 図でoはabの中点、∠oca=∠odbのとき aoc≡ bodとなることを証明せよ。 三角形の合同証明の総合的な練習問題です。定期テスト対策や高校入試対策としてもご利用ください。三角形の合同証明のポイント基本的な合同条件、証明のやり方をしっかり確認してから取り組んでください。 三角形の合同 二等辺三角形 直角三角形1合同なることを証明する三角形を囲ん
証明 (合同・相似)が苦手な人へ 教遊者 IC Channel 192K subscribers Subscribe 中2,中3,受験生平行と合同,三角形と四角形,相似「証明 (合同・相似)が苦手な人へ90%以上の証明に使えるテンプレートと素材まとめ」デジタル板書データ Watch later九去法の応用例 次の二つの計算のうち、一つだけ正しいが、どちらでしょうか = 次の証明のどこがおかしいのかを見つけてください。73 ひとつの応用例 中国の剰余定理には様々な応用があるが,ここでは,2 次合同式 (1) x2 227x354 0 (mod 504) の整数解を考えよう.素朴に考えれば,x に0;1;2;
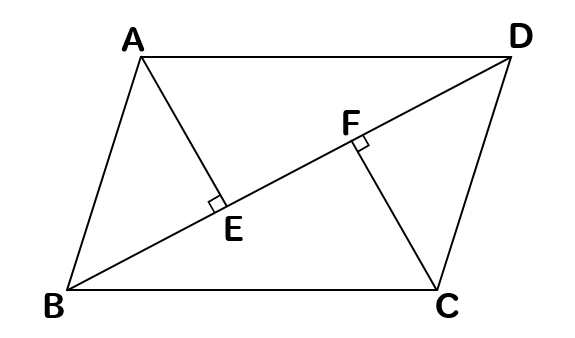
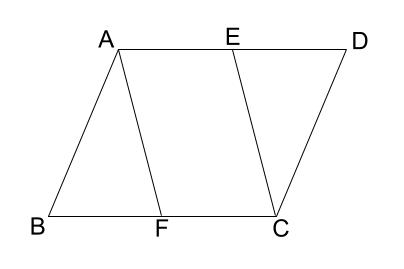
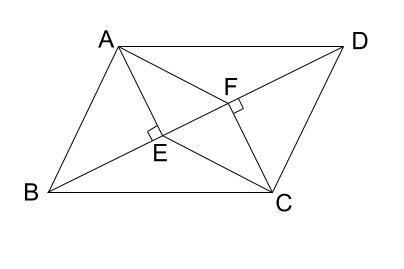
平行四辺形の性質を使った証明 三角形の合同 問題(1 学期中間) 平行四辺形abcd のa,c から対角線bd にひいた垂線とbd との交点をそれぞれe,f とする。中学数学 平行と合同の内容 z 平行線と角 z 対頂角 z 同位角と錯角 z 三角形の角 z多角形の角 z図形の合同 z 三角形の合同条件 z 仮定と結論 z 証明 *「ページ表示」を「見開き」でご覧いただきますと、問題とその 答えが見やすくなります。合同な三角形の対応する辺は等しいので be=df abe と cdf において ab=cd(abcd の対辺) ∠abe=∠cdf(abcd の対角) be=df(仮定) よって 2組の辺とその間の角がそれぞれ等しいので abe≡ cdf 合同な三角形の対応する辺は等しいので ae=cf aeo と cfo において



Studydoctor三角形の合同証明の進め方 中2数学 Studydoctor




三角形の合同条件を使った証明問題 中学2年生の問題を解こう 身勝手な主張
直角三角形の合同条件と証明問題です。 直角三角形の合同条件 直角三角形の合同条件はつぎの2つになります。 (直角三角形は1つの角が直角と分かっているので、残りの2つの角はともに鋭角になります。 ) 斜辺と1つの鋭角がそれぞ 16年8月12日 証明(合同) 1枚ずつ印刷 証明 練習用シート 証明 練習用シート(フリー) 「三角形の合同の証明」の手順をつかむための練習シートです。 abc、 defに長さや角度、記号などを自由に書き込んで、証明の問題を作ってご利用くださいませ。証明のすすめ方(5) 5 三角形・四角形 二等辺三角形の性質(1) 問題一括 (4,155Kb) 解答一括 (4,859Kb) 二等辺三角形の性質(2) 二等辺三角形の性質(3) 2つの正三角形 二等辺三角形になるための条件(1) 二等辺三角形になるための条件(2) 定理の逆 直角三角形の合同(1)



中学数学証明問題です 直角三角形の合同条件はわかるのですが Yahoo 知恵袋



中学2年数学練習問題 直角三角形の合同条件と証明問題 図形と合同
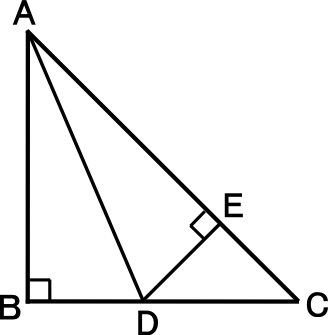
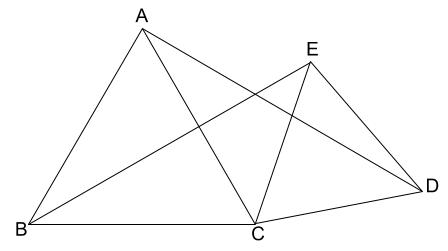
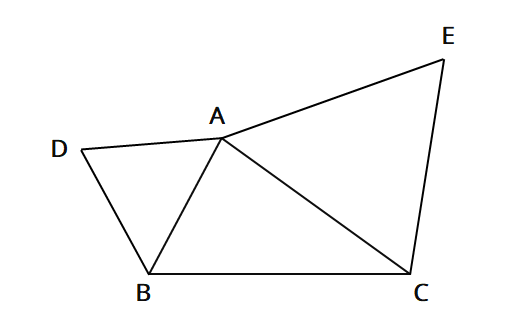
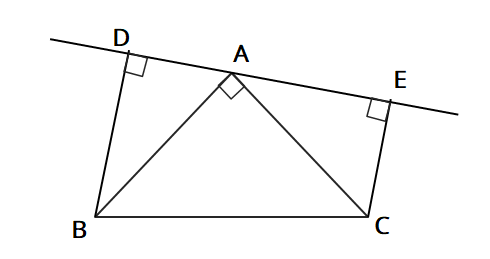
三角形証明 (発展1) 図の ABCはAB=AC,∠BAC=90°の直角二等辺三角形である。 ADEはAD=AE,∠DAE=90°の直角二等辺三角形である。 このときBD=CEを証明しなさい。 次の図のような ABCがある。 辺AC上に点Dがあり、BCの延長上にEがある。 点Dを通り辺BCに平行な直線をnと今回は、中2で学習する証明問題の単元から 平行四辺形の証明問題について取り上げていくよ! 平行四辺形の証明問題とは、大きく分けて以下の2つだね 平行四辺形の性質を利用した合同の証明; そのためには、 図形の証明で使う最低限の知識(図形の性質、合同条件等)を頭に叩き込んで下さい。大した量ではありません。その後、「証明の書き方」を覚えます。 テンプレート化しちゃうんです。 あとは基本の証明問題を10問練習し模試レベルに移行。




โน ตของ 受験対策 図形の性質 合同 証明 ช น Junior Clear



平行四辺形の性質1
中学数学の合同証明の問題で質問です。 この問題の証明の仕方を教えてください。 abcの辺ac上に点dをとる。da=db=dcならば角abc=90°であることを証明せよ。 よろしくお願いしま中2数学。2つの「辺の長さ」が等しいことを証明せよ。ヤバいこれも合同証明? それとも違うの? 図形はムズカシイ(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 証明問題はコツがある!(ビシッ)無料サイトだ。三角形の合同の証明の利用 四角形 \(abcd\) が平行四辺形であることを示すために、 辺の長さ、角の大きさが等しいことを示したいときがあります。 これを示すために、 「三角形の合同を証明し、そこから示す」 ということ




錯角 同位角 対頂角の意味とは 平行線と角の性質をわかりやすく証明 応用問題アリ 中2数学 遊ぶ数学




中学数学 証明 二等辺三角形であることの証明 中学数学の無料オンライン学習サイトchu Su
三角形の合同の証明(応用)中2数学 問題をノーヒントでやってみよう 略解をチェックしよう 攻略ポイントを確認しよう ・証明の手順に慣れよう ・等しい角の表し方に慣れよう 完璧じゃなかったら授業動画を見よう やる気先生の授業動画 直角三角形の合同と錯角を利用します。 平行四辺形(2) 平行四辺形を対角線を利用して証明するパターン。 平行四辺形であることを証明するのに例としてよく出る形ではあるのでしっかりと練習しておきましょう。 これこそが、図形問題なのである。 測ったらタルトが本当に45度で切られていて見事だった 肩慣らしとして、これを解いてみよう。 出題は、「xの角度を求めよ」。 三角形の内角の和は180度。 かつタルトは二等辺三角形なので、角ABCは (180度45度)/2 = 675




数学証明コツ Mp3




この様な中学二年生で習う 応用問題である証明問題での質問です この証明問題は Clear
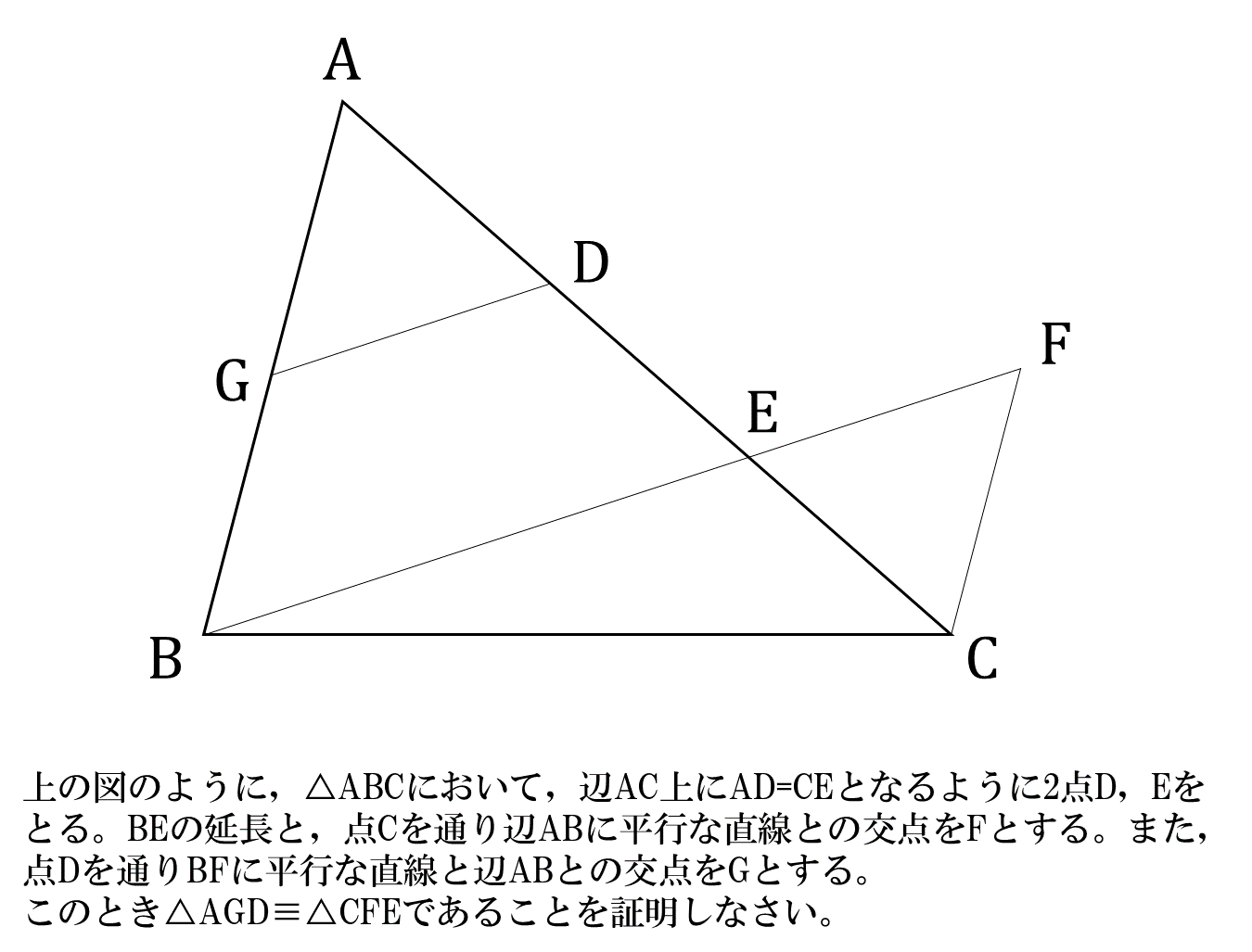
どの三角形の合同を証明すべきか(17年度北海道) このブログは「図がシンプルだけど結構キツイ問題」を紹介する目的で最初は作りました。 だんだん色々な問題を紹介するようになりましたが。 今回は,初心に戻って,非常に図がシンプルだけど,何指数の理論の応用として,合同方程式の解の存在に関する次の定理を得る. 定理 30 を 素数 証明 を解くには を法とする原始根 をとって (234) を解けばよい. 今 とする.定理 12 から, この合同方程式 が解を有するための必要十分条件は, が で三角形の合同を証明することで、その対応する辺が等しいことを言えます。 この証明の定番パターンは以前に学習していますね。 \(ad,ae\) をそれぞれ辺とする三角形を探しましょう。 そしてそれらは合同であると言えそうでしょうか?




中2 中3 三角形と四角形 相似 合同 相似の証明でよく出る応用問題 デジタル板書データ Youtube



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ
合同式(mod)を使うメリット 表記簡略化による本質的な嬉しさ 「 12 12 12 と 7 7 7 を 5 5 5 で割った余りは等しい」と書くよりも 「 12 ≡ 7 (m o d 5) 12\equiv 7\pmod{5} 12 ≡ 7 (mod 5) 」と書く方が楽です。 ほとんど差がないように感じますが,記述式で複雑な問題になると上記のような文言を大量に 応用問題を解くには、当然、基本が分かっていないとできません。 ということで、まずは相似(合同)や比の問題で最初にやることを確認しておきます。 ①与えられた長さ、角度、比は図に書き込む ②比を求めたい場合は、比を求めたい直線を、1辺とし 証明のポイント ①条件をすべて満たしていることを示す。 ②その根拠も必ず示す。 この二つのポイントがわかっていれば、図形の証明もばっちりです。 合同の証明をしてみよう では実際に合同の証明をしてみましょう。



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




D Descubre Como Resolverlo En Qanda
「うわー、応用パターンかー・・・」と不安になるかも知れないけど、実は全然こわくないよ。 合同な図形って、 「辺の長さ」 も 「角の大きさ」 も 「すべて等しい」 んだよね。 ということは結局、 今まで通りに「合同」を証明 してやることができれば、「辺」や「角度」の等しさも証明



中学数学 平行四辺形の証明問題を徹底解説 数スタ
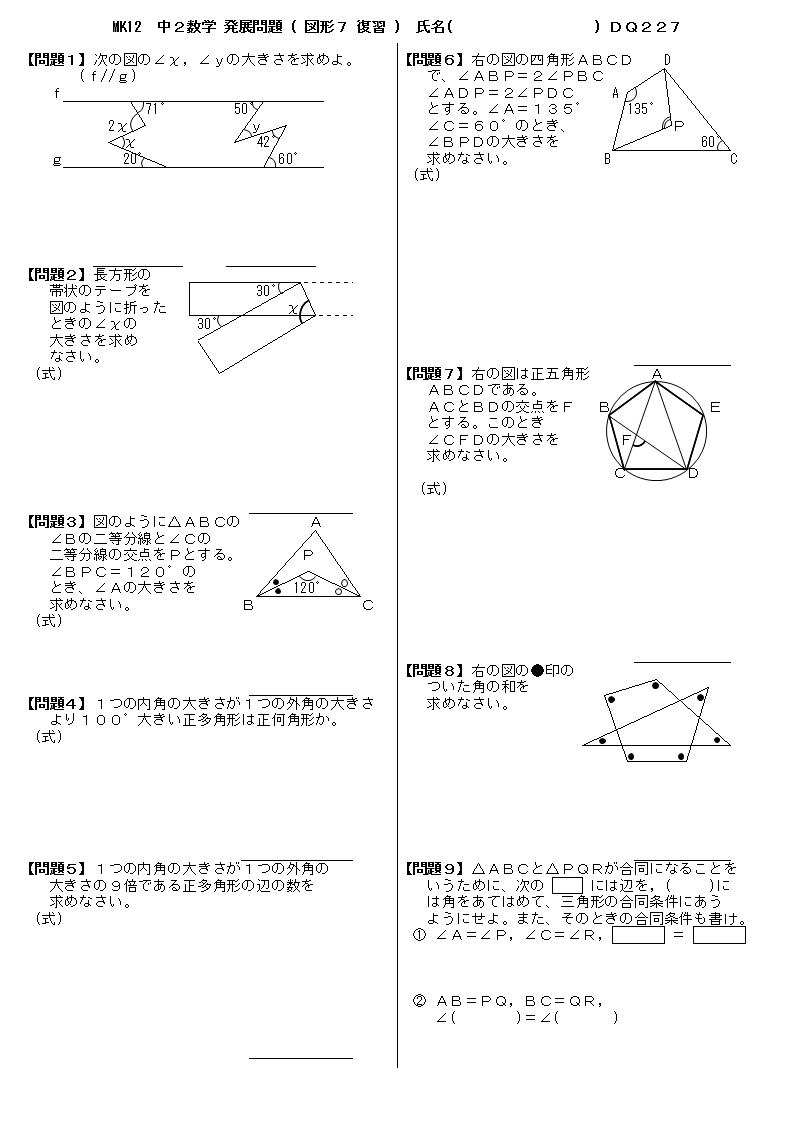



無料 中2数学 応用 発展問題 問題プリント 327 図形の相似2 相似条件と証明



Studydoctor三角形の合同証明の進め方 中2数学 Studydoctor




三角形の合同証明の練習 無料で使える中学学習プリント




働きアリ



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ



中学数学 正三角形の性質を利用した証明 中学数学の無料オンライン学習サイトchu Su
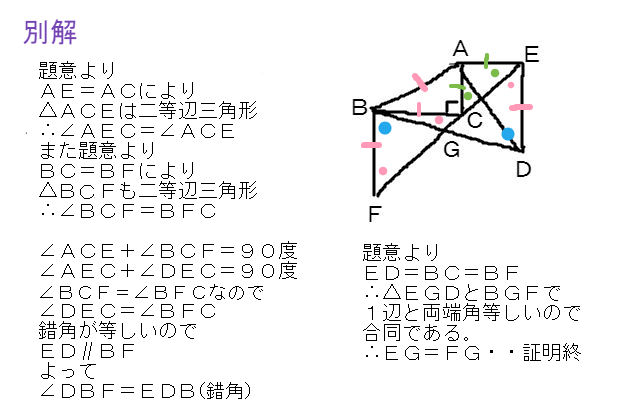



三角形の合同の応用問題 制限3分 中学数学 理科 寺子屋塾の復習サイト




三角形の合同の応用 算数 数学が好きになりmath
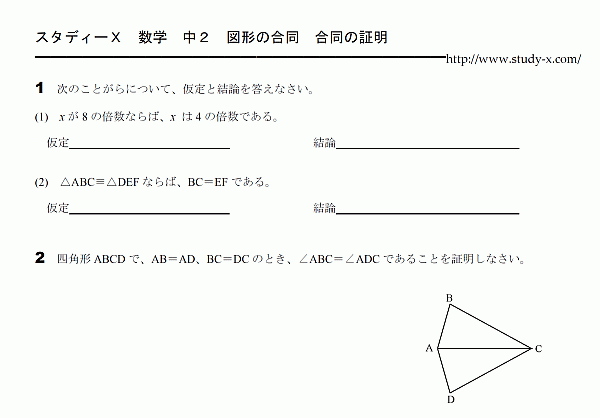



中2 数学 無料学習プリント教材



U9j580gf8iba369ji2w Xyz P 608



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ



合同な図形 三角形の証明問題 苦手な数学を簡単に




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学




中2数学 三角形の合同条件2 2辺とその間の角 練習編 映像授業のtry It トライイット




中2数学 二等辺三角形の証明 例題編 映像授業のtry It トライイット



中2数学 三角形の合同の証明応用問題 中学生勉強サイトあかね先生



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su



直角三角形と証明 中学2年 数学クラブ
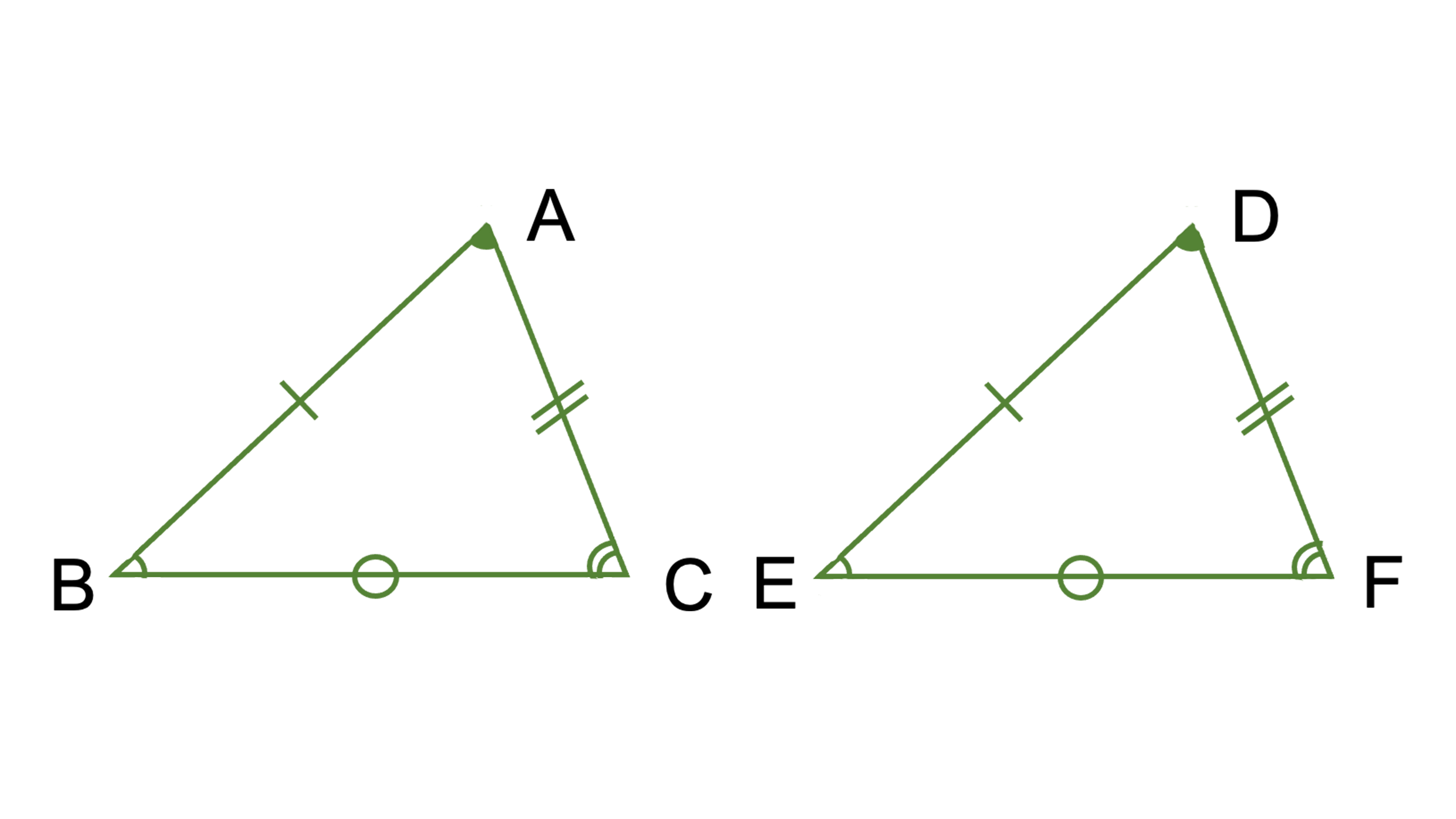



三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




平行四辺形の証明問題 無料で使える中学学習プリント
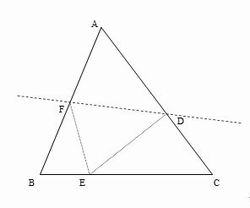



入試対策 図形の証明問題は意外と簡単だ 駿英式 勉強術
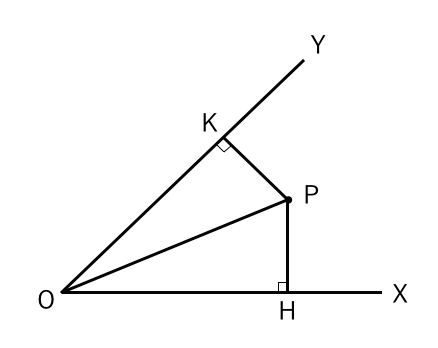



直角三角形の合同 証明問題 苦手な数学を簡単に




直角三角形の合同条件を使った証明とは なぜ2つ増えるのか 遊ぶ数学



3




数学 時短演習cote




三角形の合同の証明 応用 中2数学 Youtube
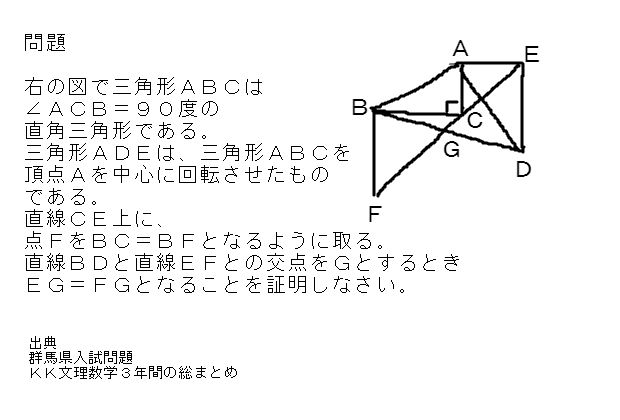



三角形の合同の応用問題 制限3分 中学数学 理科 寺子屋塾の復習サイト



特別な平行四辺形2



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典



中2数学 直角三角形の合同の証明 応用問題 中学生勉強サイトあかね先生



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su




年第3回実力テスト 数学 応用問題 中学3年生 赤城 ᐡᐤᐡ




世界一わかりやすい数学問題集中2 5章 図形の性質と証明




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中学数学 証明 二等辺三角形の性質の利用 中学数学の無料オンライン学習サイトchu Su



数学 中学証明問題を解く4つのポイント




平行四辺形になることの証明 Youtube
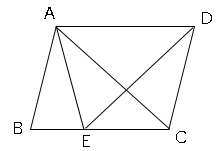



平行四辺形の合同の証明問題と角度を求める問題 数学の要点まとめ 練習問題一覧




中学数学が秒でわかる 正三角形の中に正三角形がある図形の証明 超 解説付き なぜか分かる はかせちゃんの怪しい研究室




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学



平行四辺形になるための証明3




発展講座 メネラウスの定理の証明とその応用 南数英指導会 南ノートブログ版



平行線と線分の比 辺の長さを求める応用問題4選 教遊者




直角三角形の合同条件を使った証明とは なぜ2つ増えるのか 遊ぶ数学
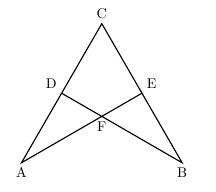



三角形の合同の問題の解法 夢を叶える塾
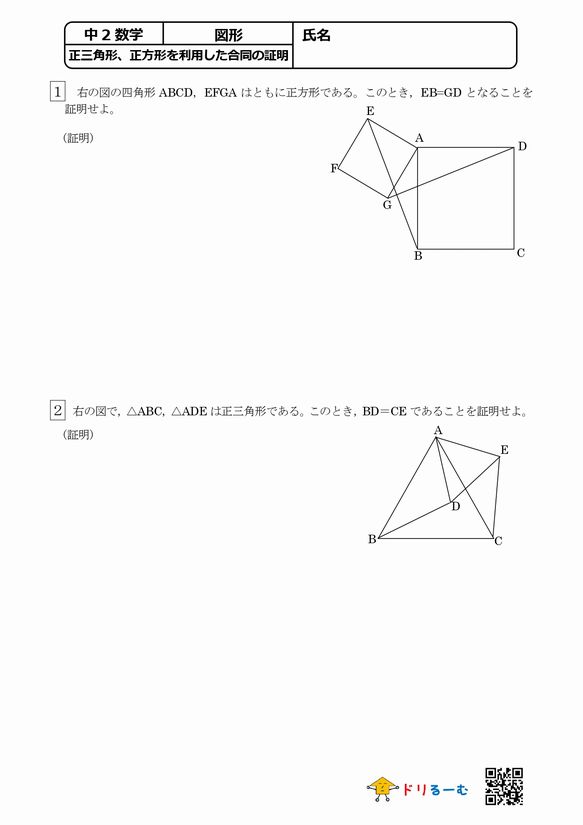



正三角形 正方形を利用した合同の証明 ドリるーむ
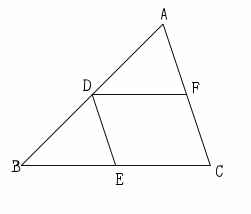



平行線の証明
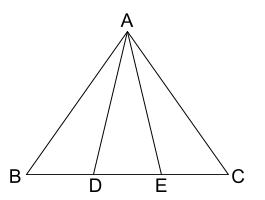



中学数学 証明 二等辺三角形の性質の利用 中学数学の無料オンライン学習サイトchu Su




Mathematics 平行と合同 証明の書き方 2 よく出る問題 働きアリ




世界一わかりやすい数学問題集中2 5章 図形の性質と証明




二等辺三角形になることの証明 Youtube




平行四辺形の証明問題 無料で使える中学学習プリント
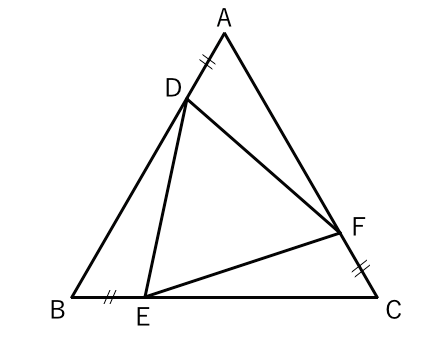



合同な図形 正三角形の証明問題 苦手な数学を簡単に
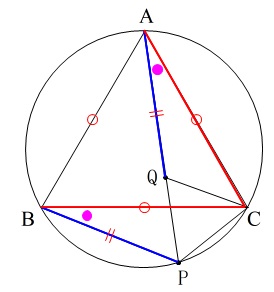



中学の図形証明問題 合同 相似 の解き方と証明の書き方ポイント



Studydoctor三角形の合同の証明 応用 中2数学 Studydoctor
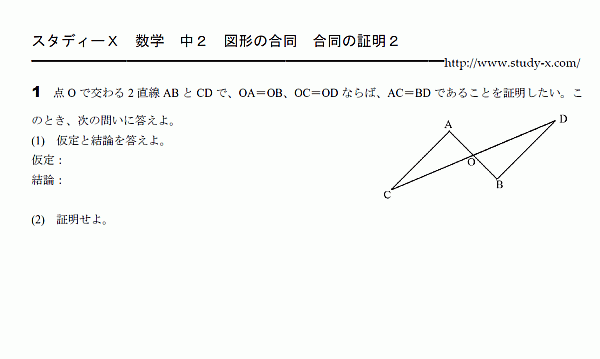



中2 数学 無料学習プリント教材




三角形の合同条件はなぜ3つ 証明問題をわかりやすく解説 相似条件との違い 遊ぶ数学



Studydoctor三角形の合同の証明 応用 中2数学 Studydoctor




Amazon Co Jp 中学 数学 2年 応用 問題集 4 平行と合同 Dvd 授業 テキスト 問題集 プロ家庭教師が教える 中学生用学習dvd 中学受験 予習 復習 試験対策 Dvd Rom Dvd



1




中2数学 三角形の合同の証明応用問題 中学生勉強サイトあかね先生




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
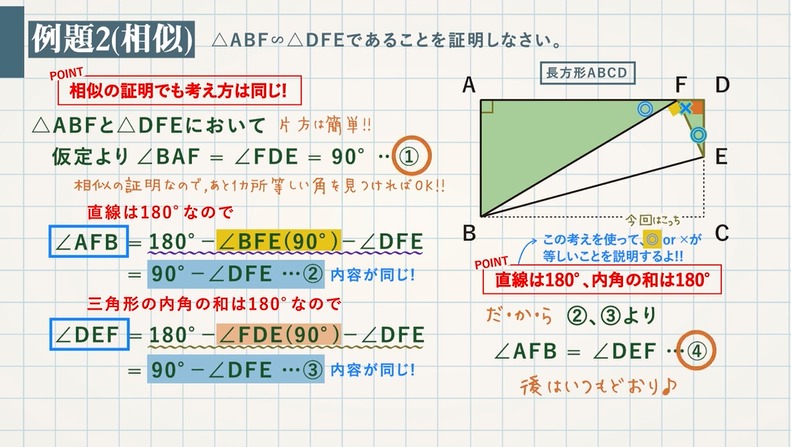



考え方はまったく同じ 合同 相似の証明でよく出る応用問題 教遊者




中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




三角形の合同証明の練習 無料で使える中学学習プリント
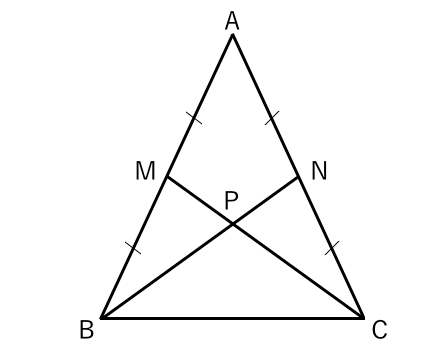



合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に



数学の証明 三角形の合同 が正しく身につく 個人契約のようなプロ家庭教師はロジティー



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ
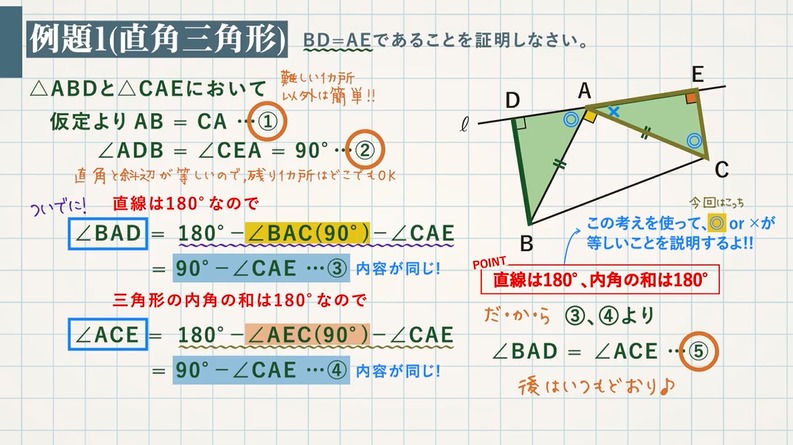



考え方はまったく同じ 合同 相似の証明でよく出る応用問題 教遊者



合同の証明 清水塾




直角三角形 清水塾



働きアリ
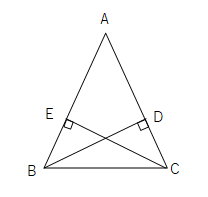



中2数学 直角三角形の合同の証明のポイントと練習問題 Pikuu
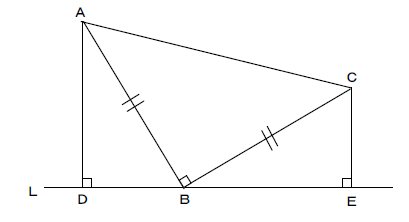



中2数学 直角三角形の合同条件を使った証明の定期テスト過去問分析問題 Atstudier




中2数学 三角形の合同を証明する問題 練習編 映像授業のtry It トライイット
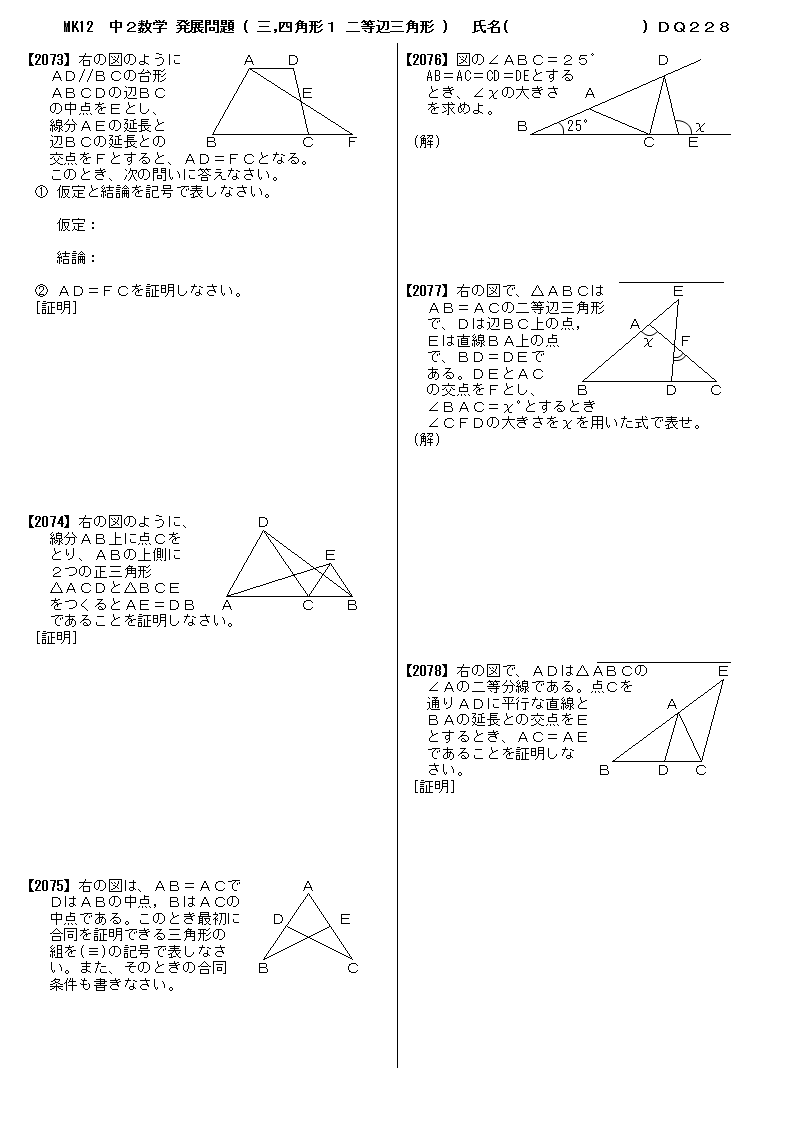



無料 中2数学 応用 発展問題 問題プリント 328 図形の相似3 線分の比




中学数学 証明問題 直角三角形 Youtube



1




三角形の合同の応用 算数 数学が好きになりmath




中2 中3 三角形と四角形 相似 合同 相似の証明でよく出る応用問題 デジタル板書データ Youtube



合同とは 三角形の合同条件 証明問題をわかりやすく解説 受験辞典
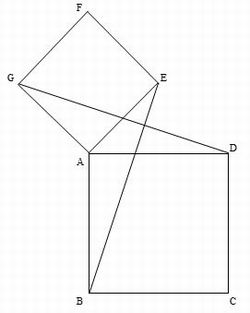



入試対策 図形の証明問題は意外と簡単だ 駿英式 勉強術




中2数学 平行四辺形の証明 練習編 映像授業のtry It トライイット




中2数学 証明とは 例題編 映像授業のtry It トライイット




正三角形の合同証明 無料で使える中学学習プリント
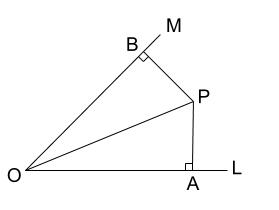



中学数学 直角三角形の合同の証明 中学数学の無料オンライン学習サイトchu Su



平行四辺形になるための証明1
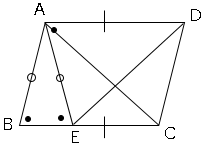



平行四辺形の合同の証明問題と角度を求める問題 数学の要点まとめ 練習問題一覧



1



0 件のコメント:
コメントを投稿