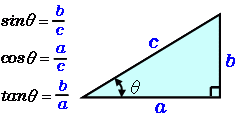
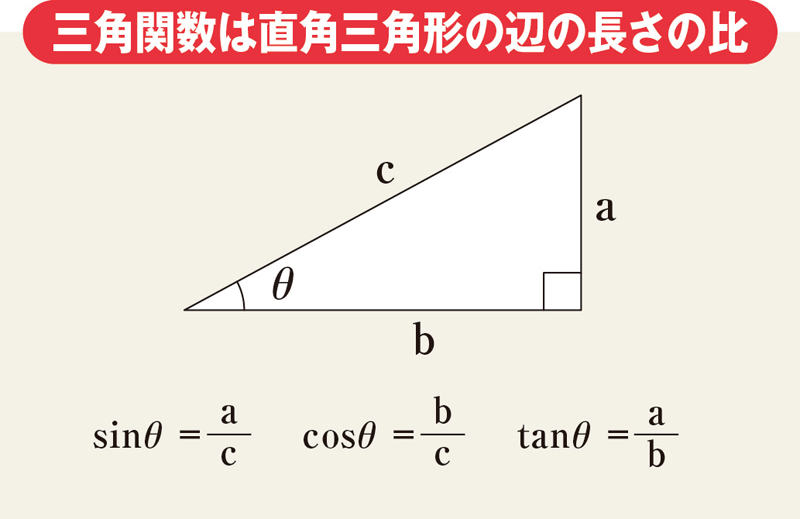
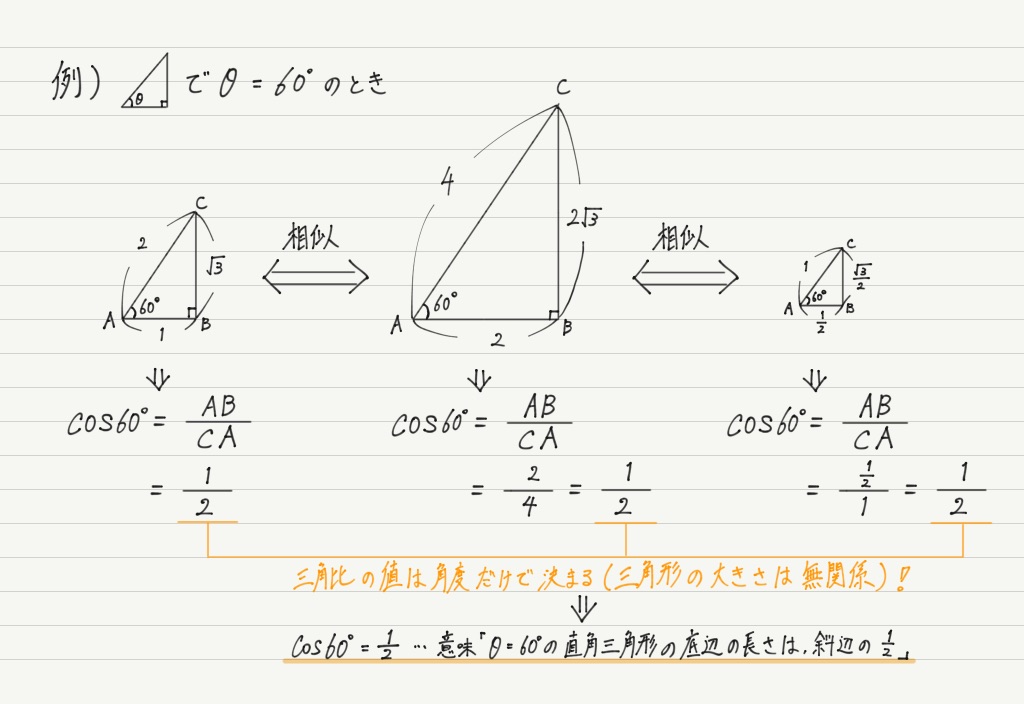
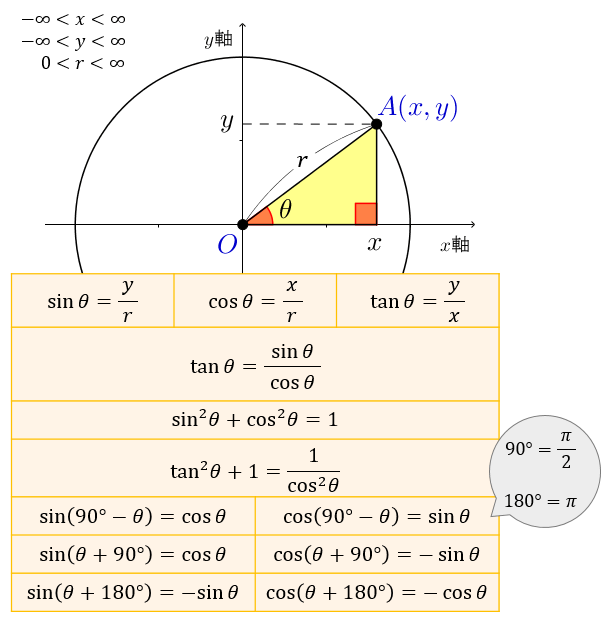
直角三角形において、1 つの鋭角の大きさが決まれば、三角形の内角の和は 180° であることから他の 1 つの鋭角の大きさも決まり、3 辺の比も決まる。 ゆえに、角度に対して辺比(三角比)の値を与える関数を考えることができる。 ∠C を直角とする直角三角形 ABC において、それぞれの辺の長三角関数の定義 原点 を中心とする半径 の円周上にある点 の座標を とする.(ただし,半径 はつねに正,座標 は正,負,0の値をとる符号が付いている) 動径 が 軸の正の向きをなす角度を とするとき,次の比の値は(相似図形の性質から)半径 の 三角関数の2倍角の公式・半角の公式の証明と応用 スポンサーリンク 高校数学Ⅱ 三角関数 検索用コード 証明は容易で,\ \bm {加法定理において\ \beta\ →\ \alpha\ }とするだけである \bm {利用機会が極めて多い}ので,\ 毎回加法定理から導くというのは

中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
三角関数 角度 公式
三角関数 角度 公式-この図もドラッグで直角三角形を移動・変形できるが、 斜辺 の長さは一定になっている。 角度と cosθ と sinθ の変化の様子を観察しよう。 この図から容易に、cos 2 θsin 2 θ=1となることがわかる(斜辺がつねに長さ1であることに注意せよ)。 sin,cosが正になったり負になったりするが、 から に/ 三角関数(度) 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 Right triangle (1) cosθ = a c, sinθ= b c, tanθ= b a (2) P ythagorean theorem a2b2 =c2 R




高校数学 三角方程式 不等式 三角関数の合成 受験の月
こんにちは。 da Vinch (@mathsouko_vinch)です。 この記事は前記事を見てから読むことをお勧めします。公式だけを知っているのは勿体無いのでぜひ寄り道してください。三角関数の合成を楽にするやり方三角関数の合成はしっか三角関数公式プラス 三角形の証明・形状問題 → 携帯版は別頁 → 印刷用PDF版は別頁 三角関数の加法定理,倍角公式,3倍角公式,半角公式 三角関数の和や積には多くの公式がありますが,「 加法定理は覚える,他は作る」 というのが,作者おすすめの tan90°が算出されないのは、そもそも値が存在しないからだと思います。 tanx=sinx/cosxのxにπ/2を代入しますとtan90°=1/0となります。 0が分母にあるのでこの値は存在しません。 よって、tan90°は存在しません。
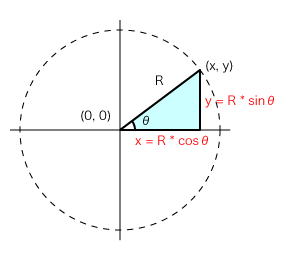
二、从上面的公式,我们知道应该用 正切。 三、计算 对边/邻边 = 300/400 = 075;角度を入力し「角度から三角関数を計算」ボタンをクリックすると、入力された角度から三角関数を計算し表示します。 三角関数は、サイン(正弦) sinθ、コサイン(余弦) cosθ、タンジェント(正接) tanθ、コセカント(余割) cscθ、セカント(正割) secθ高知工科大学基礎数学シリーズ3 「三角関数」(改訂版) −6 − < 鈍角の三角比1 > 角度θが90 以上の場合の三角比を 次で定める。 正の数r に対し,点Q(r,0) を原点 O(0,0) を中心として反時計まわりに角 度θだけ回転した点をP(X,Y) とする。
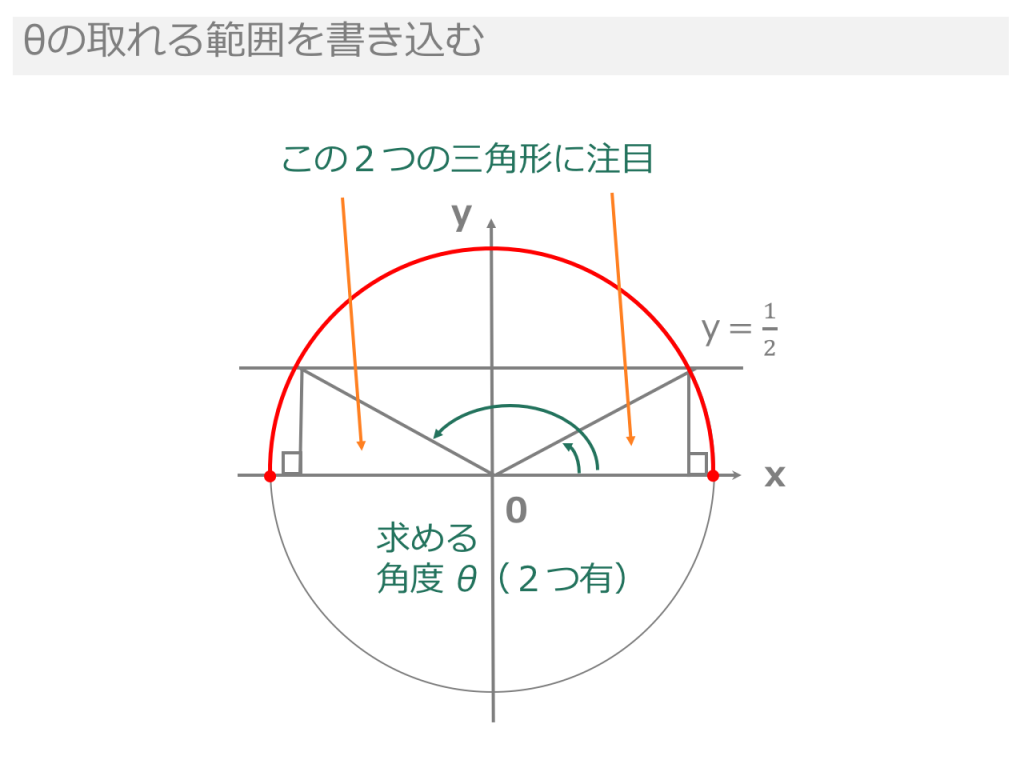
1 三角関数の角度の求め方、三角方程式の解き方 2 三角関数の角度を求めるsin編 21 三角関数の角度sinを求める①:単位円を利用する 22 三角関数の角度sinを求める②:sinθ=aのときy=aをグラフに書く この公式は15°など通常では求められないような角度の三角関数の値が求める他、 「三角関数の次数を1次下げる」ことに使われます。 (参考)半角の公式の覚え方&使い方を解説!大学入試でよく見る形を解説 三角関数の3倍角の公式倍角,三倍角,半角の公式 加法定理から導出できる三角関数のいろいろな公式です。 毎回導出してもよいですし,時短のために覚えてもよい公式です。 倍角の公式: sin 2 x = 2 sin x cos x \sin 2x=2\sin x\cos x sin2x = 2sinxcosx cos 2 x = 2 cos 2 x − 1 = 1




三角関数の公式一覧




三角関数の知識 やさしい電気回路
直角三角形の定義とさまざまな公式 レベル ★ 基礎 平面図形 三角比・三角関数 更新日時 直角三角形 とは,1つの角が直角である三角形のことです。 直角三角形のさまざまな性質を紹介します。 目次 三平方の定理(ピタゴラスの定理)Tan x° = 对边/邻边 = 300/400 = 075 tan1 of 075 = 369° (保留一位小数)三角関数2|偏角の変換公式は覚えるな! 簡単に導く方法! が成り立つことを説明しましたが,この三角比の角度の変換公式は三角関数でも同様に成り立ちます. ( 90 ∘ θ) などの変換公式も出てきます. これらの公式は非常に多いため,全部を



三角関数 度 高精度計算サイト
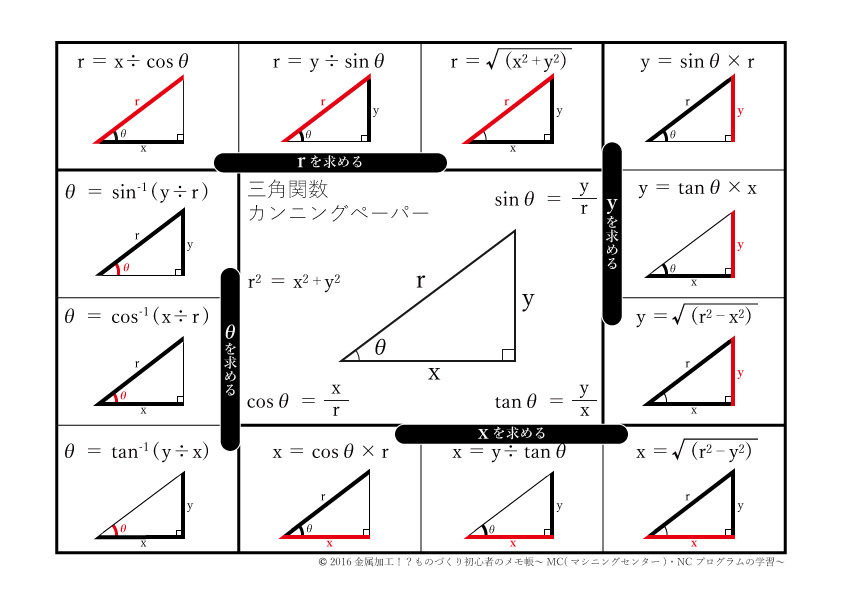



三角関数をマスターしよう その3 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習
三角関数の変換公式 ここでは、三角関数の角度の変換公式(\(90^\circ − \theta\), \(180^\circ − \theta\) など)を示します。 これらの公式は丸暗記する必要はなく、単位円を使って自分で確認できればOKです! 0 はじめに 三角関数について思うこと 三角関数というと高校時代に苦しだ方も多いかもしれません。とにかく公式も多くて、最初のうちは何に使えるのかよくわからない印象を抱きがちです。しかし実際は、理系であればいかなる分野に💅 三角関数では角度から各々の数値を取得していたわけですが、 逆三角関数では数値から角度を計算することができるのです。 この値域の範囲を「主値」といいます。 2 逆余弦関数の微分公式の導出 1 と同様にして微分公式を導出することができます。



三角関数の角度は 3分でわかる求め方 公式と計算 表との関係




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に
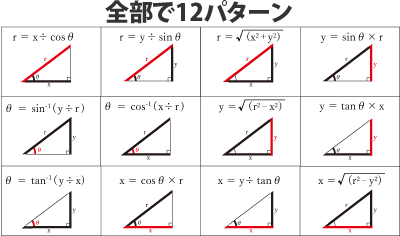
三角関数の角度に関する公式についてここでは, 以下のような公式について説明します など 数学の教科書には, このようなタイプの公式がたくさん出てきます もちろん可能であればすべて覚えてもいいですし, 毎回加法定理に当てはめて導くこともできますですが, 角度のずれの部分は など・直角三角形(斜辺と角度) 直角三角形の斜辺と角度から、底辺と高さと面積を計算します。 三角関数 ・角度から三角関数 角度(度またはラジアン)から三角関数を計算します。 ・三角関数から角度(逆三角関数) 三角関数から角度(逆三角関数)を計算します。三角関数の公式 (さんかくかんすうのこうしき)は、 角度 に関わらず成り立つ 三角関数 の 恒等式 である。



4 2 三角関数 Yasushi Noguchi Class



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ
三角関数(グラフ) sin、cos、tanの関数表を計算し、sinとcosのグラフを表示します。 逆三角関数(度) アークサイン、アークコサイン、アークタンジェントなどの逆三角関数を度単位で計算します。 角度と底辺から斜辺と高さを計算 三角形の辺の長さなどから角度(角の大きさ)を求める方法です。 次の2パターンに分けて説明します。 パターン1:3辺の長さから角度を求める方法 パターン2:2辺の長さと1つの角度から残りの角の大きさを求める方法 メインで活躍する公式は第二余弦解説2 図で示す方法 注意 積→和の公式は、のように同種の三角関数の和差です。 合成公式は、係数は付きますが1つの角度についての asinθbcosθの形です。 a・sinθb・sinθ




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座



3
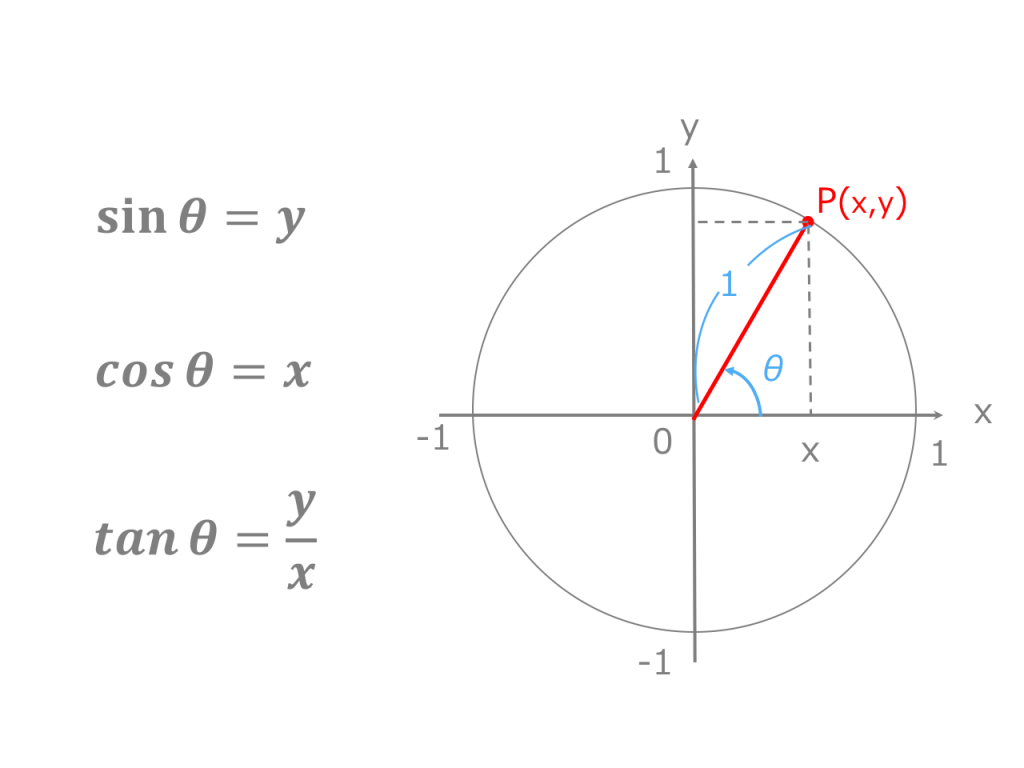
三角関数の基本 まずは超基本の三角関数の公式から確認します。 原点 を中心とする半径 の円を描きます。 軸の正の方向(つまり右)に対して、線分 による角の大きさを とするとき、 三角関数の公式 , , このように表される三角比の関数のことを応用分野: べき級数, 三角関数の不等式の解き方, 三角方程式の解き方, 三角関数 和積の公式, 次数下げの基本式, 加法定理, 問題リスト ←このページに関連している問題ですSin (θ-α)のグラフ(解説) (振幅) (周期) (周期と振幅) 三角関数のグラフ (総合1) 三角関数のグラフ (総合2) 加法定理,倍角公式,3倍角公式,半角公式 加法定理の練習問題 2倍角公式半角公式




16 合成公式はsinだけじゃないんです 医学生gの数学ノート




高校数学 三平方の定理による三角関数の計算 2 映像授業のtry It トライイット
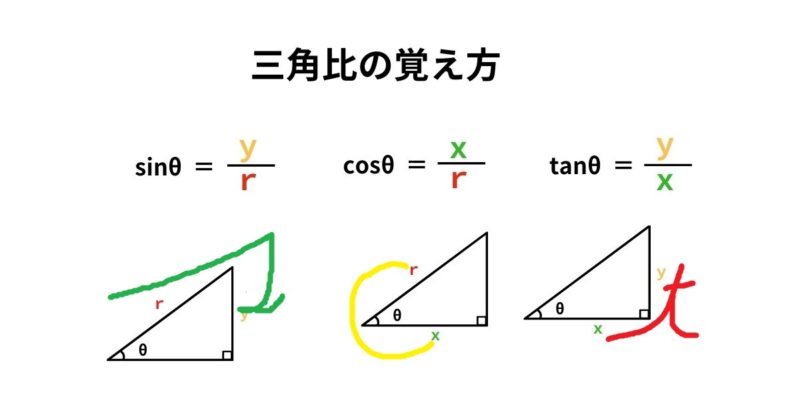
で表される3つの三角比の関数のことを、三角関数と言います。 「\(\sin{θ},\cos{θ},\tan{θ}\) の分母・分子をド忘れしそう」と感じる方も多いかもしれませんが、これらはその 頭文字 s,c,t の筆記体 のイメージと結びつけると覚えやすくなりますよ。 余弦定理は、「2辺の長さとその間の角度」から「残り1辺の長さ」を求めたり、「3辺の長さ」から「3つの角度」を求めるのに使います。 を考えたとき、直角三角形 \(acd\) に注目すると、三角関数 2倍角の公式・半角の公式とその証明。二等辺三角形で概要 この公式の名前は、18世紀の数学者レオンハルト・オイラーに因むが、最初の発見者はロジャー・コーツとされる。 コーツは1714年に () = を発見した が、三角関数の周期性による対数関数の多価性を見逃した。 1740年頃、オイラーは、コーツの公式を基に、指数関数と三角関数の級数展開




三角関数の公式一覧




直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo
三角関数の周期性と対称性から得られる公式 三角関数には、周期性と対称性があります。この性質より、以下の関係式が得られます。 なお、周期性とは、角 θ の大きさに対して、関数(sin θ, cos θ, tan θ)の値が、一定の θ の間隔で繰り返されることを言います。三角関数2|偏角の変換公式は覚えるな!簡単に導く方法! 三角関数3|「ラジアン」の考え方,公式はシンプル!←今の記事 三角関数4|有名角の三角関数は覚えるな!図で判断するコツ 三角関数5|三角関数のグラフは縦や横から見るべし! 三角比・三角関数の公式一覧。 正弦・余弦・加法定理など このページでは、 三角比・ 三角関数 の公式 をまとめています。 予習・復習に役立てていただければ嬉しいです。




三角関数の合成公式 証明 問題 Cos型について 理系ラボ
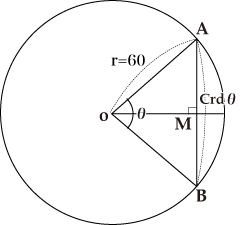



コラム 三角関数表 江戸の数学
三角関数の角度を計算する場合、「エクセル」を使うと便利です。 θ=Arcsin (038)のような半端な辺の比に対する角度も計算できます。 まずエクセルのセルに「= ASIN (038)」と入力してください。三角形の証明・形状問題 → 携帯版は別頁 三角関数の合成公式 a sin θb cos θ の形の式は一つの三角関数にまとめることができます.これを三角関数の合成公式といいます. a sin θb cos θ= √a2b2√nnnnni sin (θα) (ただし, α は cos α=三角関数 公式α,β を実数とするとき以下が成り立つ。 sin(αβ) = sinαcosβ cosαsinβ cos(α β) = cosαcosβ −sinαsinβ 証明平面上で角度θ の回転を表す行列をR(θ) と書くと R(θ) =



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ




三角関数の合成公式 証明 問題 Cos型について 理系ラボ
すなわち、角度$\theta$の補角は$\pi\theta$となる。 この補角に対する三角関数の変換公式を通称「補角の公式」という。 公式一覧 今回は、角度$\theta$に関する余角$\pi\left(\theta\right)=\pi\theta$に関する式も加えると、「補角の公式」は、下記の通り。




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ



家電やスマホに必須 三角関数は陰の働き者 中高数学おさらい 三角関数 数列 文系でも怖くない 学び直し 数学 ダイヤモンド オンライン




高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト



三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
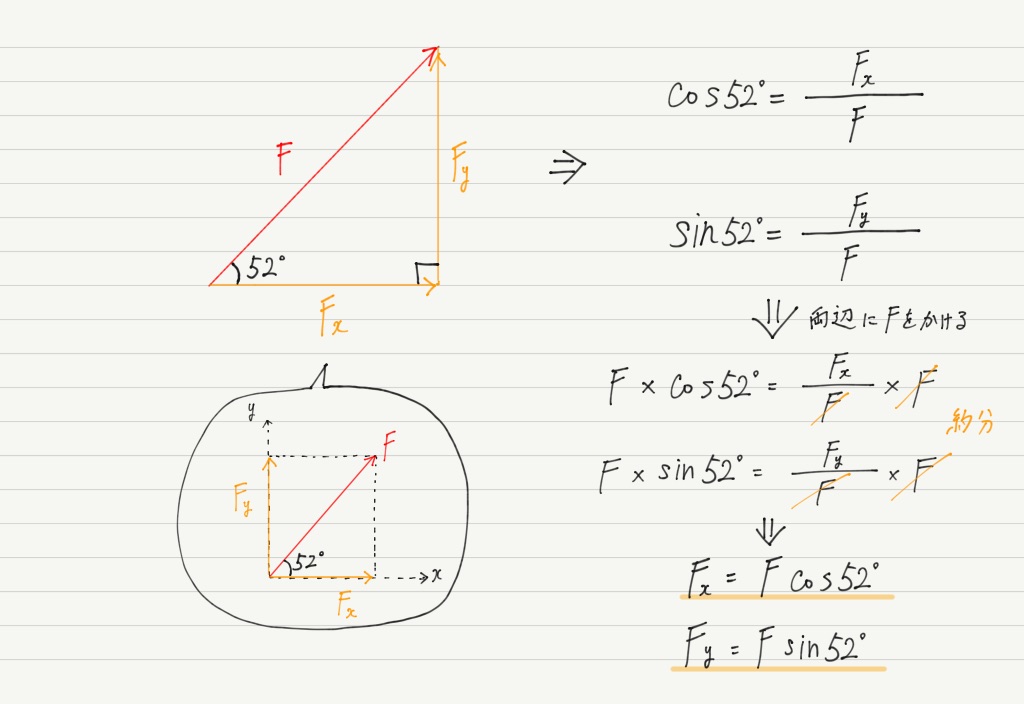



力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に




タンジェントとは何か 中学生でも分かる三角関数の基礎




三角関数の知識 やさしい電気回路




三角形の角度を求める問題 小学生 中学生の勉強




黄金三角形による18 シリーズの三角比 おいしい数学
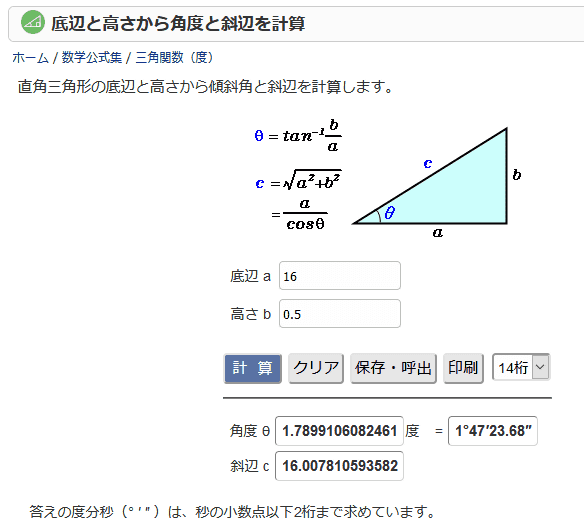



表計算ソフトを使って 底辺 と 高さ から 角度 を求める




三角形の辺から角度を計算 製品設計知識
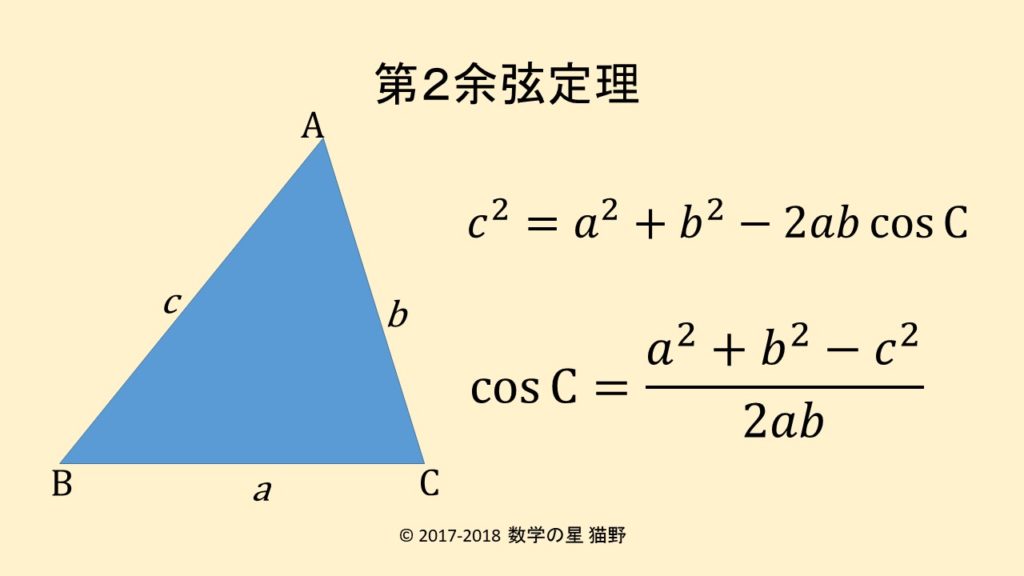



第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星




高校数学 三角比 余弦定理の公式を証明 図を使って丁寧に説明 数学の面白いこと 役に立つことをまとめたサイト



3




三角関数の公式の一覧 Wikipedia




三角関数の基礎知識
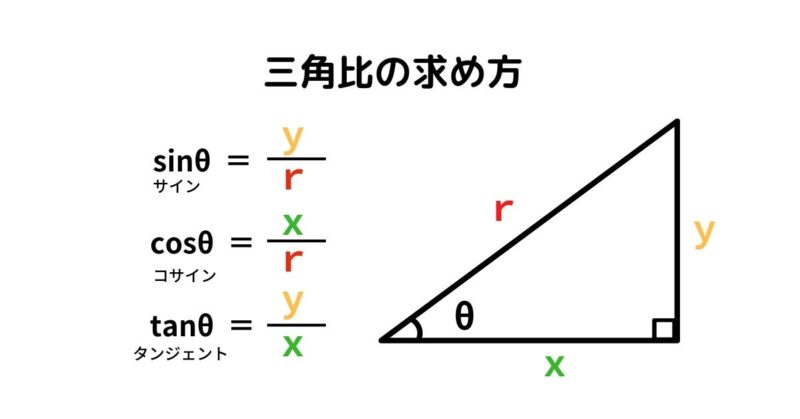



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




三角関数の合成の公式 Schoolmath S Diary



三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に
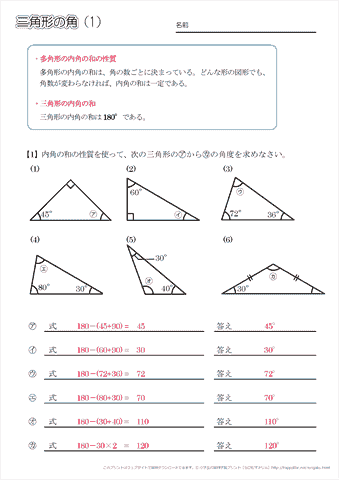



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




三角関数 重要公式




三角関数と公式 Notes Jp



三角関数をマスターしよう その2 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習




タンジェントとは何か 中学生でも分かる三角関数の基礎




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信



三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ




三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典




三角形の3辺から角度を計算 高精度計算サイト



1
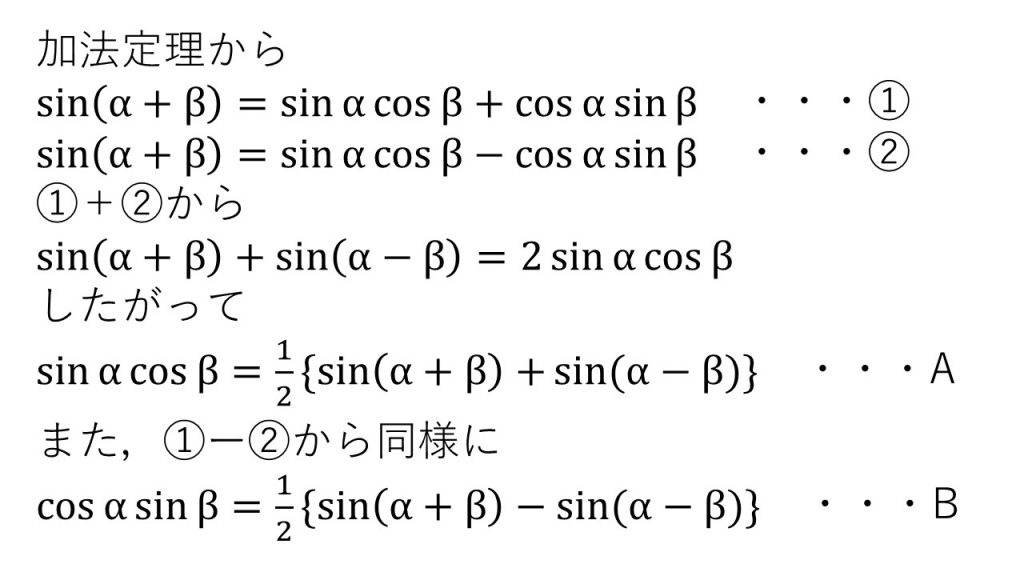



三角関数の和と積の公式 大学受験の王道



3
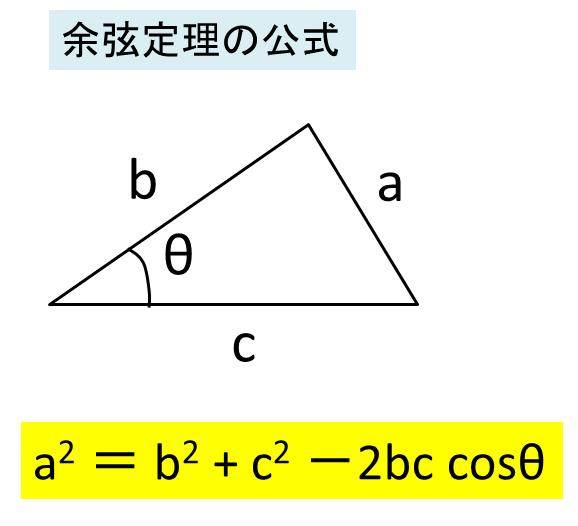



Excel エクセルで余弦定理の計算をする方法 角度や辺の長さを求める




三角関数を使った測量士補試験の計算問題 中山祐介の土地家屋調査士 測量士補 合格 ブログ



正確な角度の測定 割り付け




わかりやすい三角比と基本公式 Irohabook




1研究中 C 数学1 三角関数 1 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ
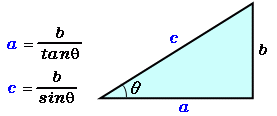



角度と高さから底辺と斜辺を計算 高精度計算サイト
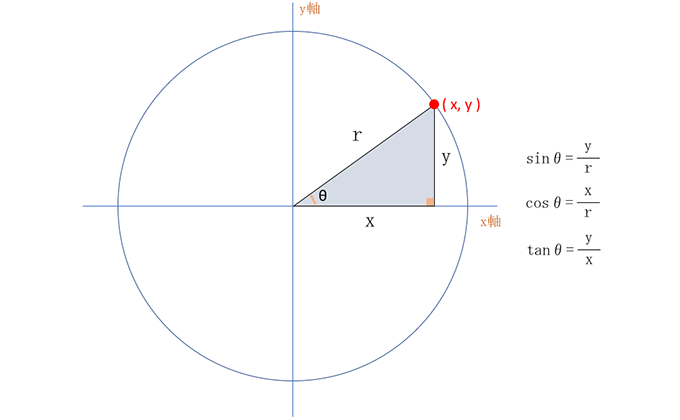



Processingで三角関数のサイン コサインを使ったアニメーション Free Style
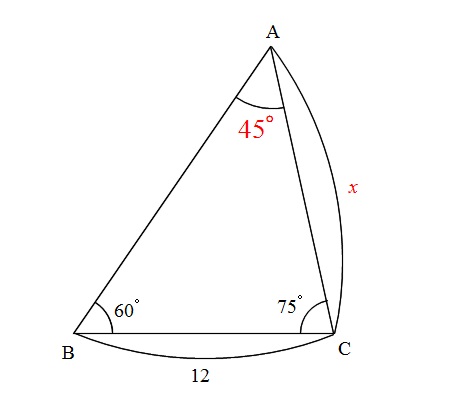



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない




三角関数で角度から座標を導くふたつの式の使い途 Qiita
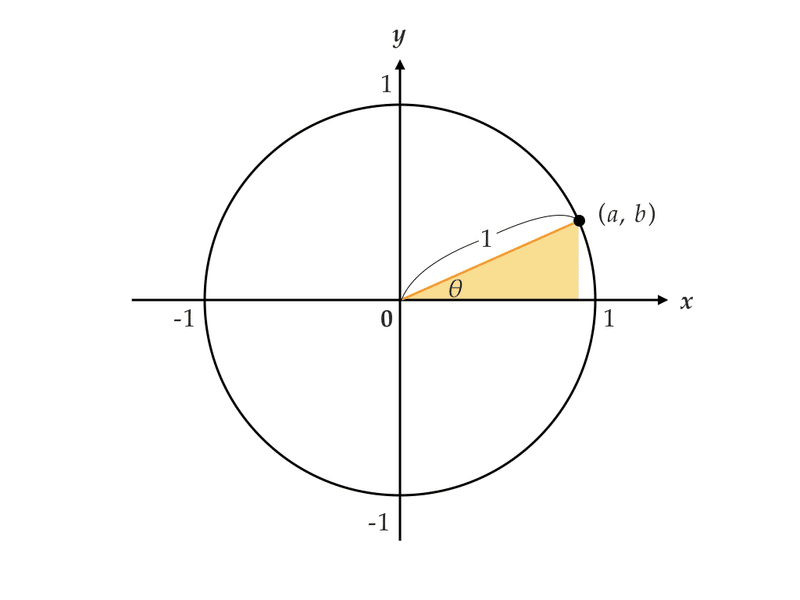



三角比 三角関数の公式を単位円と関連づけて理解する 関谷 翔 Note




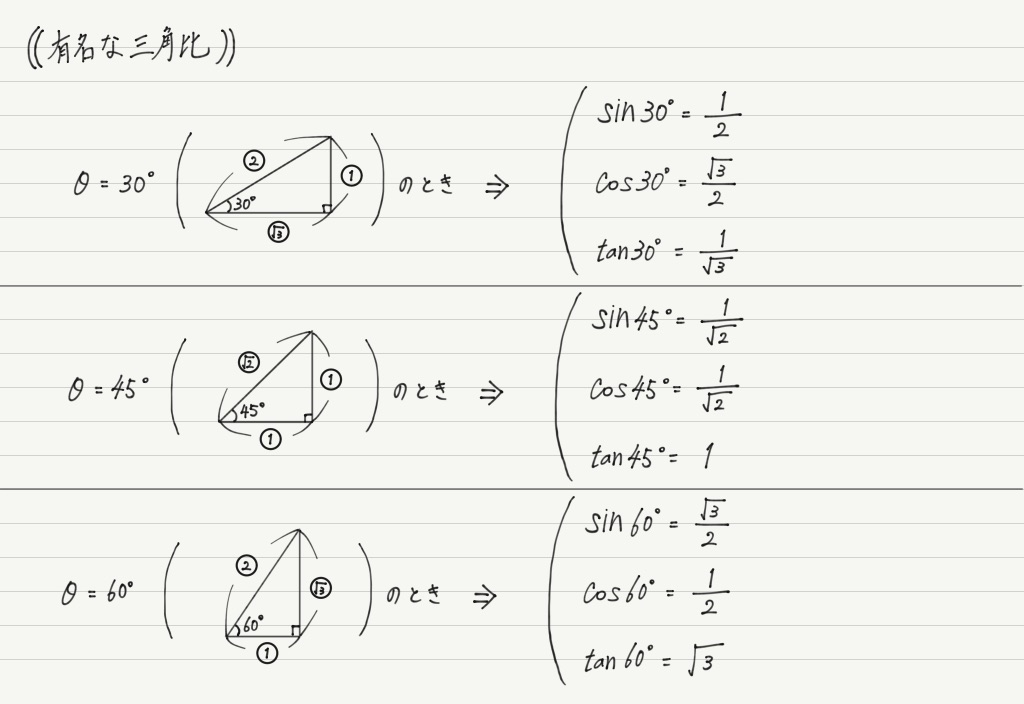
高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




底辺と高さから角度と斜辺を計算 高精度計算サイト
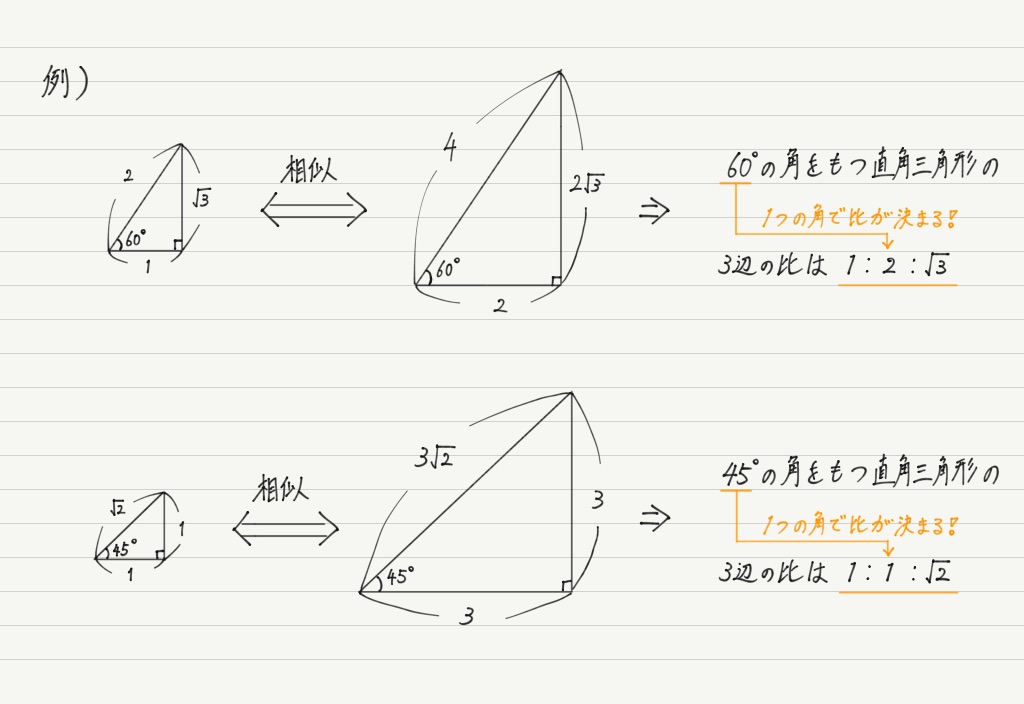



三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に
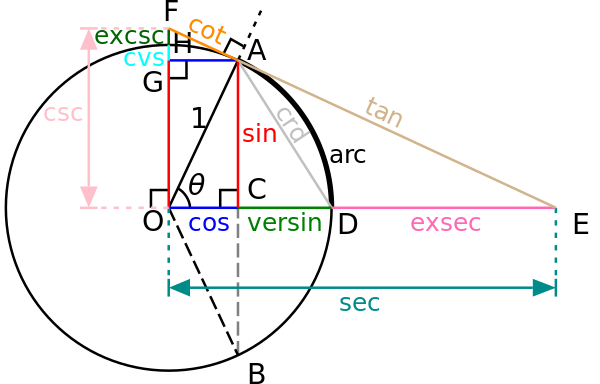



大学受験数学 三角関数 公式集 Wikibooks
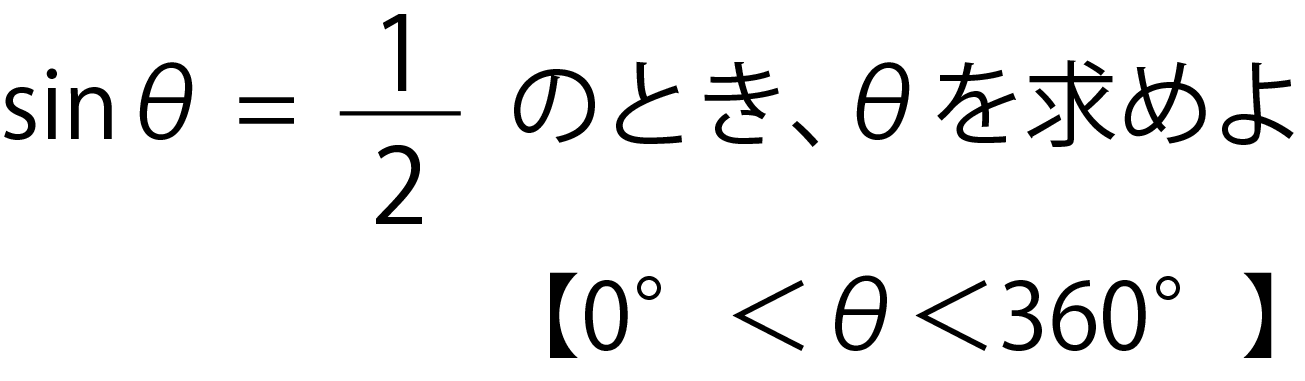



三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ



三角関数の公式 図的理解




三角関数の性質で公式を使わないやり方でやってるんですが Sin8が90度の角度の時が Clear



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典



工業用 三角関数計算ツール



三角比 三角関数を総まとめ 定義や各種公式 重要記事一覧 受験辞典




小5 算数 小5 31 三角形の角 Youtube
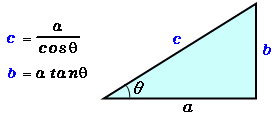



角度と底辺から斜辺と高さを計算 高精度計算サイト




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



数2 三角関数 性質



日曜大工で使う数式




Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算




高校数学 三角比からの角度の求め方1 Sin8 映像授業のtry It トライイット



直角三角形の角度の求め方 教えて下さい 斜辺以外の2辺の長さが分かっ Yahoo 知恵袋



Windows電卓で三角関数を計算する方法 Trismegistuslabo トリメギブログ




三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ




三角関数は何に使えるのか サイン コサイン タンジェントの活躍 Qiita




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




高校数学 三角方程式 不等式 三角関数の合成 受験の月



直角三角形の斜辺の長さと角度が分かっている場合 他の2辺の長さを求めたいので Yahoo 知恵袋
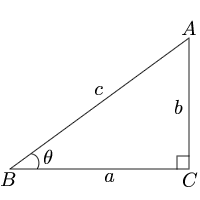



三角関数から角度 逆三角関数 三角形の計算 計算サイト




5分でわかる 余弦定理の公式と証明 使い方を簡単に理解しよう 高校生向け受験応援メディア 受験のミカタ




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト
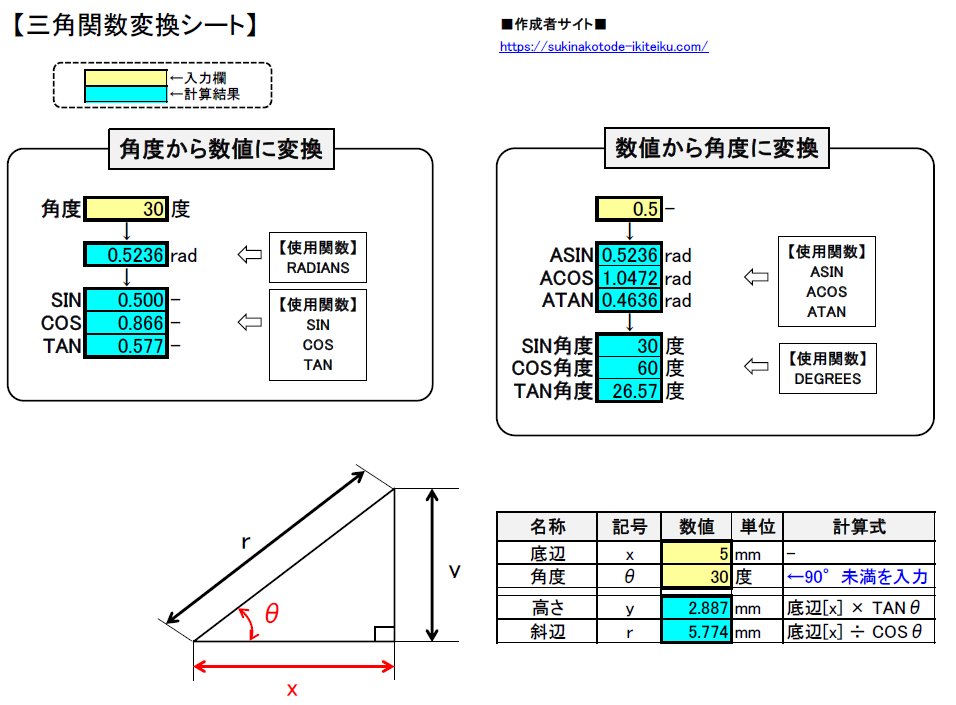



03 機械設計 エクセルで三角関数を使って角度や長さを求める Radians関数 Degrees関数 好きな事で生きていく
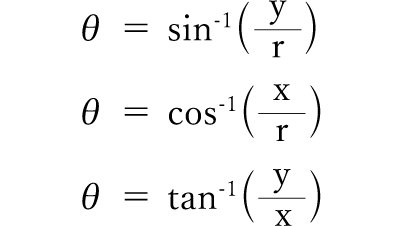



三角関数をマスターしよう その3 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習




余弦定理で角度を求める方法 数学の星
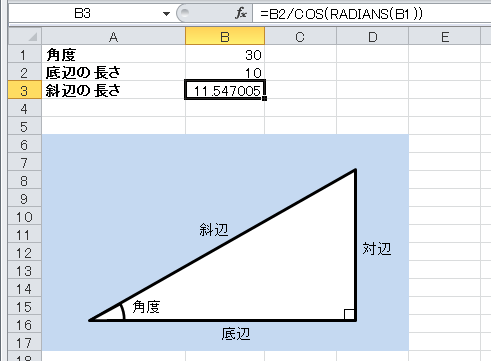



角度からコサインを計算するには Cos Radiansの解説 エクセル関数リファレンス
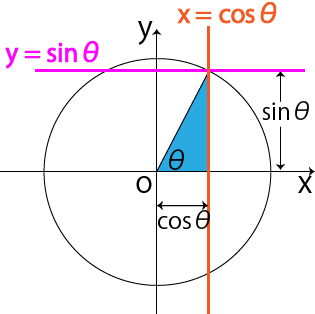



三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ
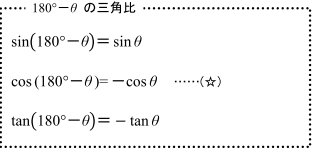



180 8の三角比 数学 苦手解決q A 進研ゼミ高校講座




機械設計でとても役立った三角関数 生産技術関連の情報ページ




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信
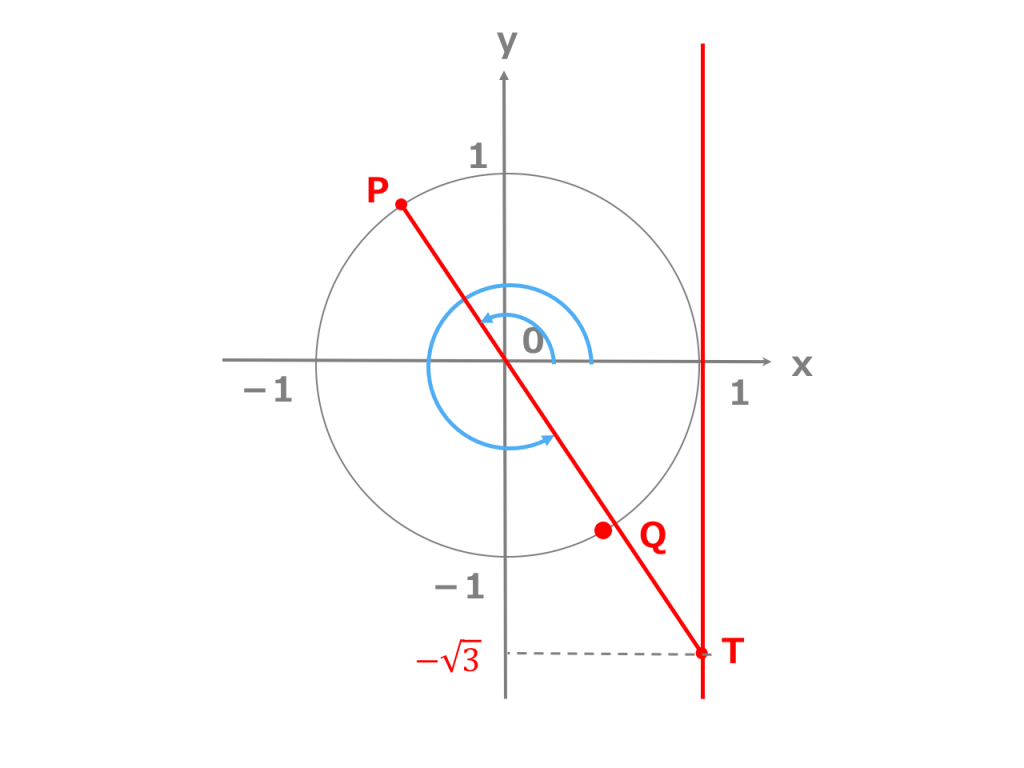



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ



三角関数とは 1分でわかる意味 公式と計算 角度と値の関係
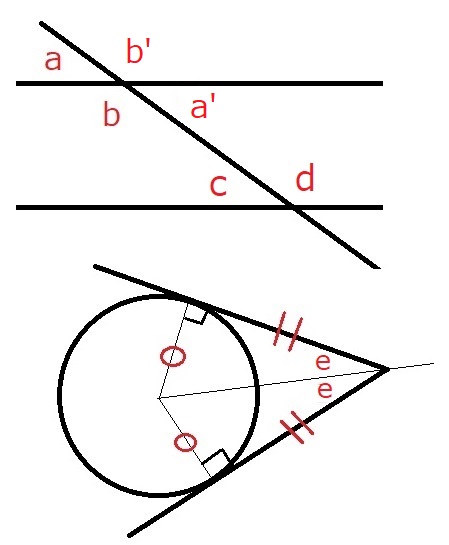



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




高校数学 数 76 三角比 基本編 Youtube




2倍角の公式と半角の公式 おいしい数学



0 件のコメント:
コメントを投稿