無理不等式の解き方 (A) 数式変形で解く方法 1 √x√ni >x−2 が成り立つためには ・ √x√ni が定義されるためには x≧0 でなければなりません.(2つのものの大小関係が言えるためには,両方とも定義されていなければなりません.)京大 数学 解き方 十勝の新築、増改築、リノベーションなら一階常微分方程式 (first order ordinary differential equations) を解く基本的な方法を整理します。 微分方程式の形によって、微分方程式の解法が異なります 。 つまり「ナントカ形の微分方程式のときは、こんな解き方で解ける! 」というパターンがいくつかあり

高校数学 定積分で表された関数の微分 D Dx F T Dt F X の証明 受験の月
F(x) 数学 解き方
F(x) 数学 解き方- 次の問題の解き方を教えてください。 f(x)=(πx)/2 (0≦x≦π) のフーリエ正弦級数と余弦級数を求めよ 数学者もしくは理論物理学者の方に質問です。研究では、紙とペンで研究を進めるのと、それ以外のもの(MapleやMathematicaなどの数式処理ソフトやMATLABなど f (x)=f (y) f (x) = f (y) なら x=y x = y が成立するとき, f (x) f (x) は単射である と言う。




2変数関数z f x y の最大値と最小値 高校数学の解き方 wolfram入力と3dプロット テンメイのrun bike
高校数学で学習する連立方程式の解き方まとめ! 文字係数の方程式の解き方まとめ! 判別式Dを使って解の個数を調べてみよう! 2次方程式の共通解、kの値の求め方はどうやる?? x軸との共有点、グラフの位置関係を考える問題を解説!F(x) の(x) は,それが「xの関数」ということを示しています。 f(x) のほかに,g(x), h(x) などが出てくることもありますが,これもニックネ-ムです。 xの関数が複数出てきたときに,それぞれ区別がつくように,それぞれ違うニックネ-ムをつけているだけ 高校数学 無料 学習サイト わかりMATH 考え方や途中式を省略しないで詳しく解説! 数学の辞書で理解が深まる! 質問するとわかりやすく教えてもらえる!
数学・算数 閲覧ありがとうございます fはR上の連続関数とする、この時関数方程式 f(x)=f(2x) を解け。 この問題が分かりません。どなたか教えてください。よろしくお願いします。おLimΣを見たら考えること どうも加藤です。 今回はlimΣについて解説していきたいと思います。 を無限級数と言います。 このlimΣ、入試では頻出です。 などなど、様々な分野と絡めやすくてlimΣの問題は差をつけやすいからです。 しかし受験生は「なんこのページでは、 数学Aの「1次不定方程式」について解説します。 1次不定方程式の整数解の見つけ方と計算方法を,具体的に問題を解きながらわかりやすく解説していきます。全部で5パターンに分けています。 問題集を解く際の参考にしてください!
3次方程式の解き方・教科書の解法 解の候補を1つだけ求める。 計算が簡単なf(1)を求めると、f(1)=0となる事が分かる。 多項式の除法 で(X 2 + X+ )を求める。 次数が3次方程式から2次方程式に下がった(バンザーイ)。 (X 2 -5X+6)を 因数 この微分の問題の解き方を教えてください 最初に f(x,y) を x で 1 回微分するとき 3重積分の問題の解き方が分かりません 数学 5大学受験数学の解き方 Part 2 数学Ⅲ 極限計算で持つべき直感 加藤 極限計算ってどこまで直感で考えていいか微妙ですよね。 例えばこんな式を見て、 \ (\displaystyle\lim_ {x\to\infty}\frac {x^23} {5x^2 数学Ⅲ limΣを見たら考えること 加藤



高2数学 次の関数の増減を調べよ という問題 答えを見たら Yahoo 知恵袋




数学iiの問題です 添付写真の問題ですが 解き方がわかりません 教わった Okwave
因数分解の例題 問題 高校の数学X 3 X 2 yXyの解き方 「共通因数をくくり出す」はできません。 「因数分解の公式を使う」もだめですね。 よって、「最低次数の文字について整理してから、因数分解する」 不等式の解き方 一次不等式の解き方中学の数学 二次関数の決定で重要なポイント解き方3パターンを覚えよう 二次関数の決定において、問題の解き方は 3 3 パターンに決まっています。 最初にまとめをしておきましょう。 一般形 y = a x 2 b x c y = a x 2 b x c 通る 3 3 点が与えられた場合に使うF (x)を求めよという問題です! 解き方がわかりません。 Clear f (x)を求めよという問題です! 解き方がわかりません。 答えはあり見ましたがわかりませんでした。 どなたかおしえてください!




3分で分かる F X の意味とは F X にまつわる様々な疑問に回答 合格サプリ



1
f(x)=10X,g(x)=30xの解き方教えて欲しいです!No1 です。「お礼」に書かれたことについて。>全部小文字です!これは #1 で聞いていることの半分にしか答えていませんよ?「また、何をどう解くのですか?」についてはどうなってい例題1 (教科書練習問題72 類題:前回演習問題) 1 階の条件を使って次の最大化問題を解きなさい。 maxf(x;y) = x2 y2 xy xy 解答例 4 制約付き最適化問題の解き方:基礎数学II(2変数をダイレク x x が任意の有理数のときに以下が成立する: f (x)=xf (1) f (x) = xf (1) 3:仕上げ




数学 極限 画像の問題をこの前解答してもらったのですが 2次関数 Ax Okwave



F X 5x 4x 2の逆関数f X を求めよ こ Yahoo 知恵袋
xの係数が偶数(2の倍数)のとき計算が楽になる。 積分路の変更原理 関数f(z)は領域Dで正則とする。単一閉曲線Cの中に単一閉曲線\(C_1\)があってCと \(C_1\) の間の領域はDの点のみからなるとする。このとき $$\int_C f(z)dz=\int_{C_1} f(z)dz$$ が成り立つ。 ここでは、\(f(x)=x^{2}5\)を使って求め方と証明をしていきます。 ここから(2)を解くには、数学的帰納法の知識が必要なので、必要な方は「数学 数列と漸化式については「漸化式の解き方 一次不定方程式の解き方 一次不定方程式 $\ a'xb'y=c'\ $ の解き方は きちんと体系化されています。 なので覚えてしまえばしまいなのに、結構皆さん覚えていません。毎度、その場その場で解き方を考えてしまっているのです。




数学の問題です 解き方を教えてください 14 F X Xの二乗 2 3 15 高校 教えて Goo




2 でf X 0になるxがないときのグラフの書き方がわかりません なぜx 0の Clear
積分のやり方と基礎公式。 不定積分と定積分の違いとは? 積分とは、「 微分 の反対」に相当する操作です。 たとえば、 F ( x) = 3 x 2 を微分すると F ′ ( x) = 6 x になりますよね。 これに対し、積分とは「 微分したら F ′ ( x) = 6 x になるような F ( x) をF (x) = 2^x f (x) = 2x 」となりますが、これは指数関数です。 e^x はtに関係ないので定数扱いで外に出すと f (x) = xe^x•∫ 0→1 f (t)e^t dt




F X の意味 数学 苦手解決q A 進研ゼミ高校講座




高校数学 3次関数の極大値と極小値の和 解と係数の関係の利用と変曲点の利用 裏技 受験の月
2次方程式x^2=aの解き方2 step1 ポイント 2次方程式x^2=aの解き方2 中3数学で学ぶ「2次方程式x^2=aの解き方2」のテストによく出るポイントを学習しよう! step2 例題 2次方程式x^2=aの解き方2 中3数学で学ぶ「2次方程式x^2=aの解き方2」のテストによく出る世界共通の方が便利なのでみんな `f(x)` を使いますが、特に何でもかまいません。 また、1つの問題で複数の関数が出てくるときは、 出てきた順に `f(x), g(x), h(x)` などと表すことが多いです。 この手の問題の解き方は、今までと同様に 「一番外のfの ()の中から崩していく」 というやり方です。 つまり f (f (x))=f (2x5) とまずは書き換えます。 そしてもともと f (x) で x だったところを 2x5 に置き換えます。



微分積分とは 高校数学の基礎から応用までわかりやすい記事総まとめ




関数方程式 高校数学演習 Youtube
部分積分の解き方とコツ。 どっちを微分するか判断するポイントとは? 関数 f ( x), g ( x) とそれらを微分した f ′ ( x), g ′ ( x) に対して成立する以下の公式を、 部分積分 と言います。 x d x を計算してみましょう。 を当てはめると、以下のように部分方程式の解き方2 「両辺に同じ数字をかけても等式は成り立つ」 この性質を利用してxに係数がある方程式を解く。 xに係数があったら、 係数の逆数 をかけて1にする。 例 方程式 –3x = 12 の解き方 xの係数は 3 なので、 両辺に3の逆数をかけて 、両辺F (x)=a (xp)²qの "p"がグラフの頂点のx座標に、"q"がグラフの頂点のy座標 になります。 つまり、 f (x)= (x1)²3のグラフは、(1,3)を頂点とするグラフである ことがわかります。




二次関数の決定とその背景 高校数学の美しい物語
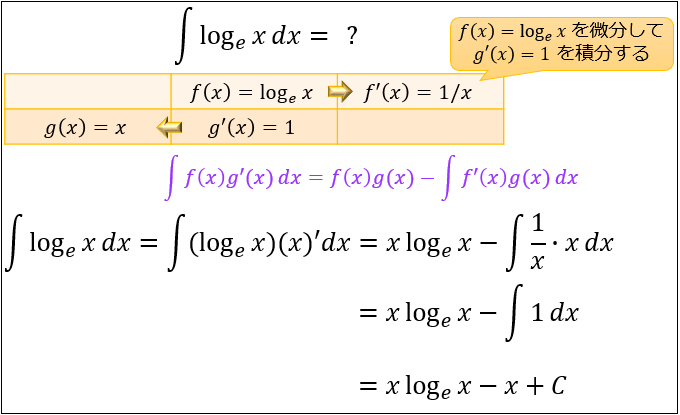



部分積分の解き方とコツ どっちを微分するか判断するポイントとは アタリマエ
f (x)の (x)は、 ()の値が、fの式のxに代入する値を指していますよね。 さあ今のを踏まえて、さらに分かりやすい問題文に変えちゃうと、 『f (x)=x+1 の時、f (x+1)=x+1の値を求めよ』 こ




高校数学 関数 F X の増減と F X の符号 映像授業のtry It トライイット




高校数学 積分方程式 変数型 3パターン 受験の月
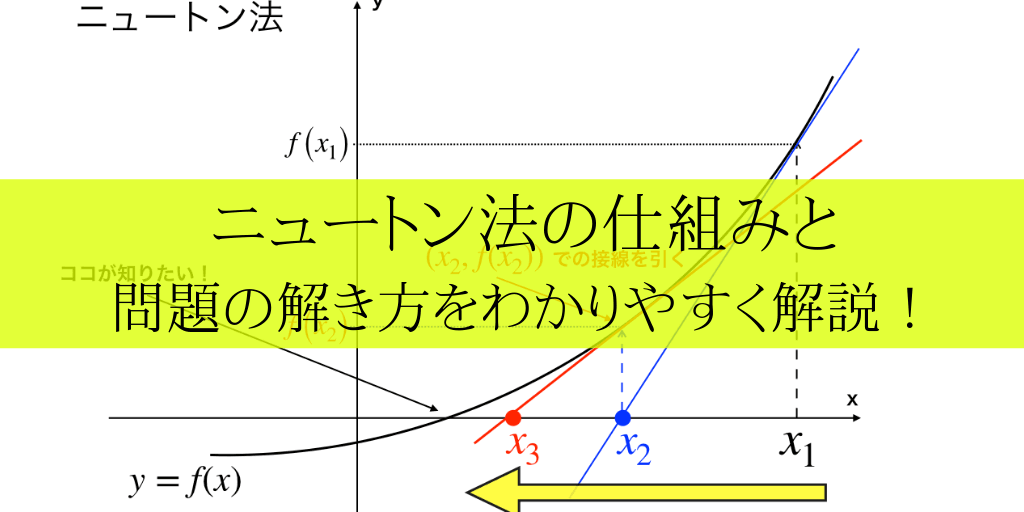



ニュートン法の仕組みと証明の仕方を分かりやすく解説




関数x Xの最小値 関数x 1 X の最大値 シュタイナーの問題 を求めてみよう 身勝手な主張




数学の問題なんですが 解き方わかる方いらっしゃいますか Clear




高校 数学 2次関数4 関数f x 7分 Youtube




解き方 センター試験数学 A 新課程 15年度大学入試数学 東大数学9割のkatsuyaが販売する高校数学の問題集




このときのf X とf T は文字を置き換えただけで形は同じ関数っていうことですか Clear




2変数の不等式の証明解法まとめ おいしい数学
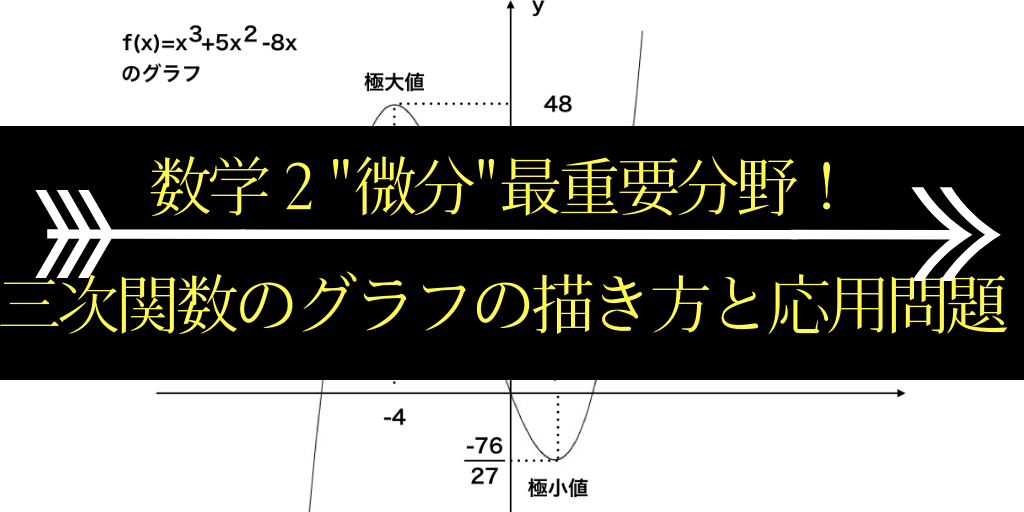



三次関数のグラフと極値の求め方 問題の解き方を解説 数学2 微分
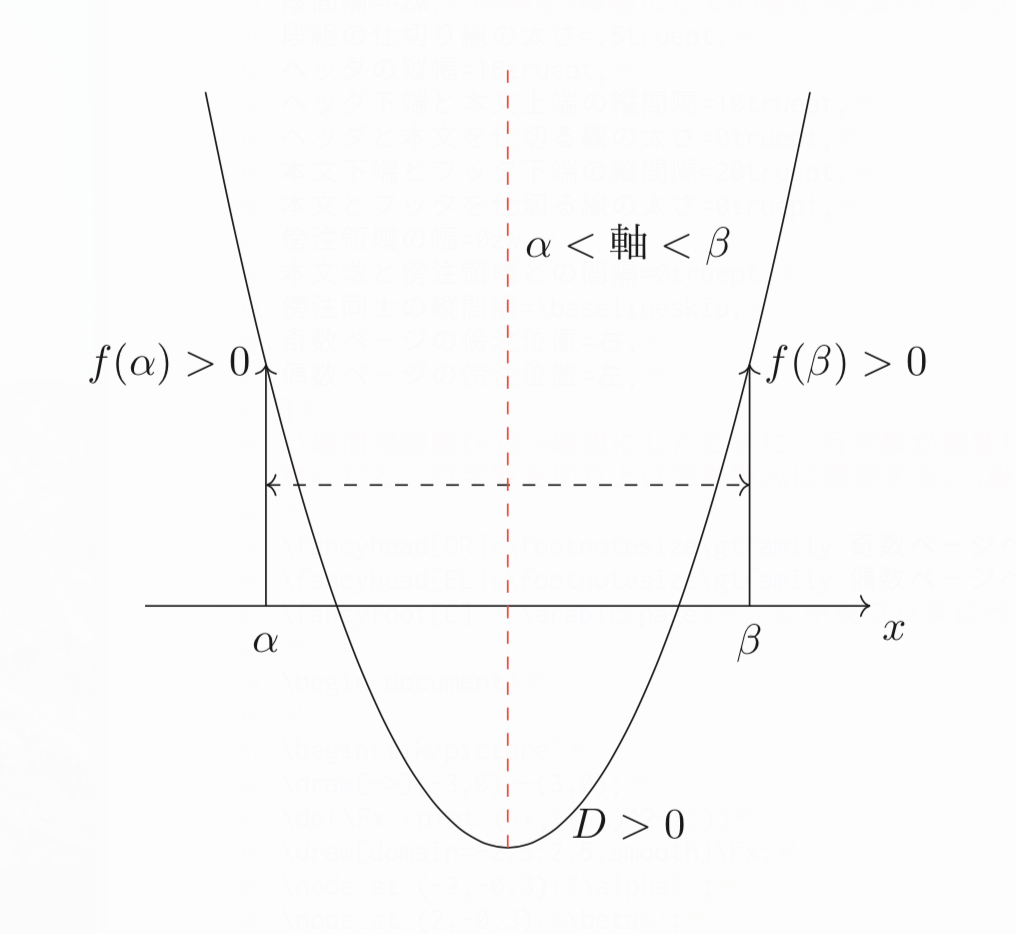



解の配置問題のパターンや解き方を例題付きで東大医学部生が解説 東大医学部生の相談室
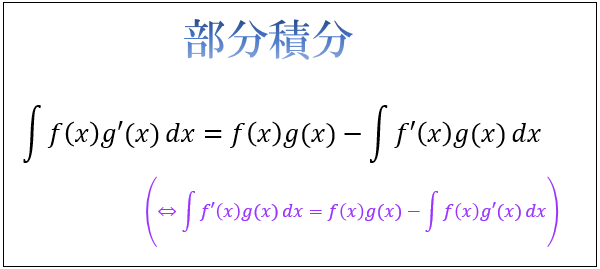



部分積分の解き方とコツ どっちを微分するか判断するポイントとは アタリマエ




高校数学 導関数 F X 例題編 映像授業のtry It トライイット




関数の値に関する入試問題 18年 兵庫県立大 大学入試数学の考え方と解法



数学ですxの整式f X があって画像の恒等式が成り立つときの解き Yahoo 知恵袋



F X の書き方について 下の二つならどちらでも大丈夫ですか Fの筆 Yahoo 知恵袋




大学受験 河合模試の過去問です 2 のf X 0とはどんなグラフでしょうか Clear




高校数学 不定積分 F X Dx 映像授業のtry It トライイット



高校生です 数学 のテストで微分の問題があるのですが このよう Yahoo 知恵袋



数学2 整関数の微分 61 東京大 数学好きの男子高校生のぶろぐ




高校数学で学習する連立方程式の解き方まとめ 数スタ



数学ll B 関数f X 9 X 9 X 2 3 X 2 Yahoo 知恵袋



Search Q A B 5e3 Tbm Isch




高校数学 定積分で表された関数の微分 D Dx F T Dt F X の証明 受験の月




高校数学 定積分で表示された関数 2 映像授業のtry It トライイット



不定積分とは 公式や計算問題の解き方 分数を含む場合など 受験辞典




数学 積分計算の型網羅part3 分数関数 理系ラボ




高校数学 関数f X とは 映像授業のtry It トライイット




この問題の解き方を教えてください Clear



1




2次関数 2次方程式の解の存在範囲と判別式 数学 定期テスト対策サイト



3




丸つけたところの解き方を教えてください Clear




高校数学 絶対値f X の定積分の値は面積 映像授業のtry It トライイット




3分で分かる F X の意味とは F X にまつわる様々な疑問に回答 合格サプリ




この数1の問題のアイウまでは分かるのですが それから先の解き方が分かりません 教えて Clear




451 3 の解き方が分かりません Clear




451 3 の解き方が分かりません Clear




この 3 の解き方を教えてください 特に余りを割っていくところが分かりません Clear




高校数学 B 積分 定積分が2個入った方程式の解き方level2 やはり俺の考察ブログはまちがっている アニメ 数学




2変数関数z f x y の最大値と最小値 高校数学の解き方 wolfram入力と3dプロット テンメイのrun bike




平均値の定理まとめ 証明 問題 使い方 理系ラボ
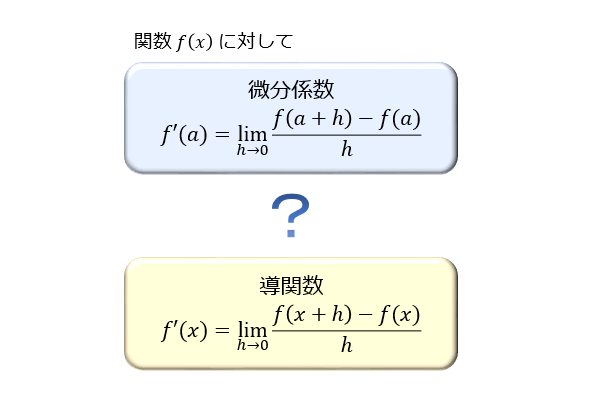



微分係数と導関数の違いとその使い分け アタリマエ



Fx高校数学問題の解決機 をapp Storeで
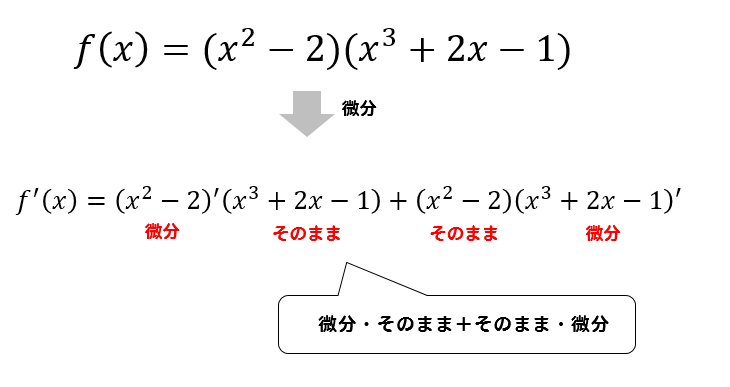



微分のやり方 計算方法まとめ 分数や三角関数のやり方は 数スタ




数学 F X G X となる範囲 すべての ある の違いを理解しておこう 数スタ




関数方程式f X Y F X F Y 型の解法とコツ 大学受験レベル




関数f X と象限 超わかる 高校数学 A 授業 2次関数 1 Youtube



三次関数とは グラフや解き方 接線 極値の求め方 微分 受験辞典




数学の問題です 解き方を教えてください 答えは 7番 X 1で極大値0 8 高校 教えて Goo




高校 数学 2次関数4 関数f x 7分 Youtube




数学大百科事典 仕事で使う公式 定理 ルール127 Amazon Com Books




F X ってなに 3分でわかる微分の基本 ともよし塾 受験と科学の解説授業
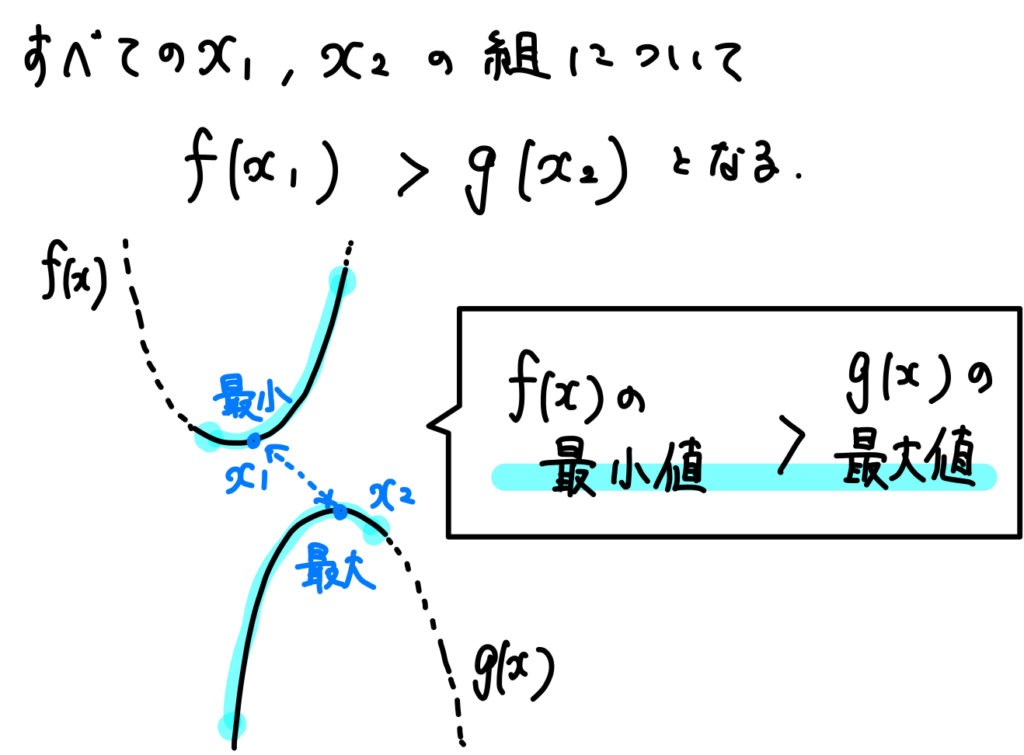



数学 F X G X となる範囲 すべての ある の違いを理解しておこう 数スタ




高校数学 関数f X の逆関数はf 1 X で表す 問題編 映像授業のtry It トライイット




関数f X とは何か わかりやすく具体例3選を通して解説します 遊ぶ数学




積分のやり方と基礎公式 不定積分と定積分の違いとは アタリマエ




高校数学 合成関数の方程式f F X Xと不動点 受験の月
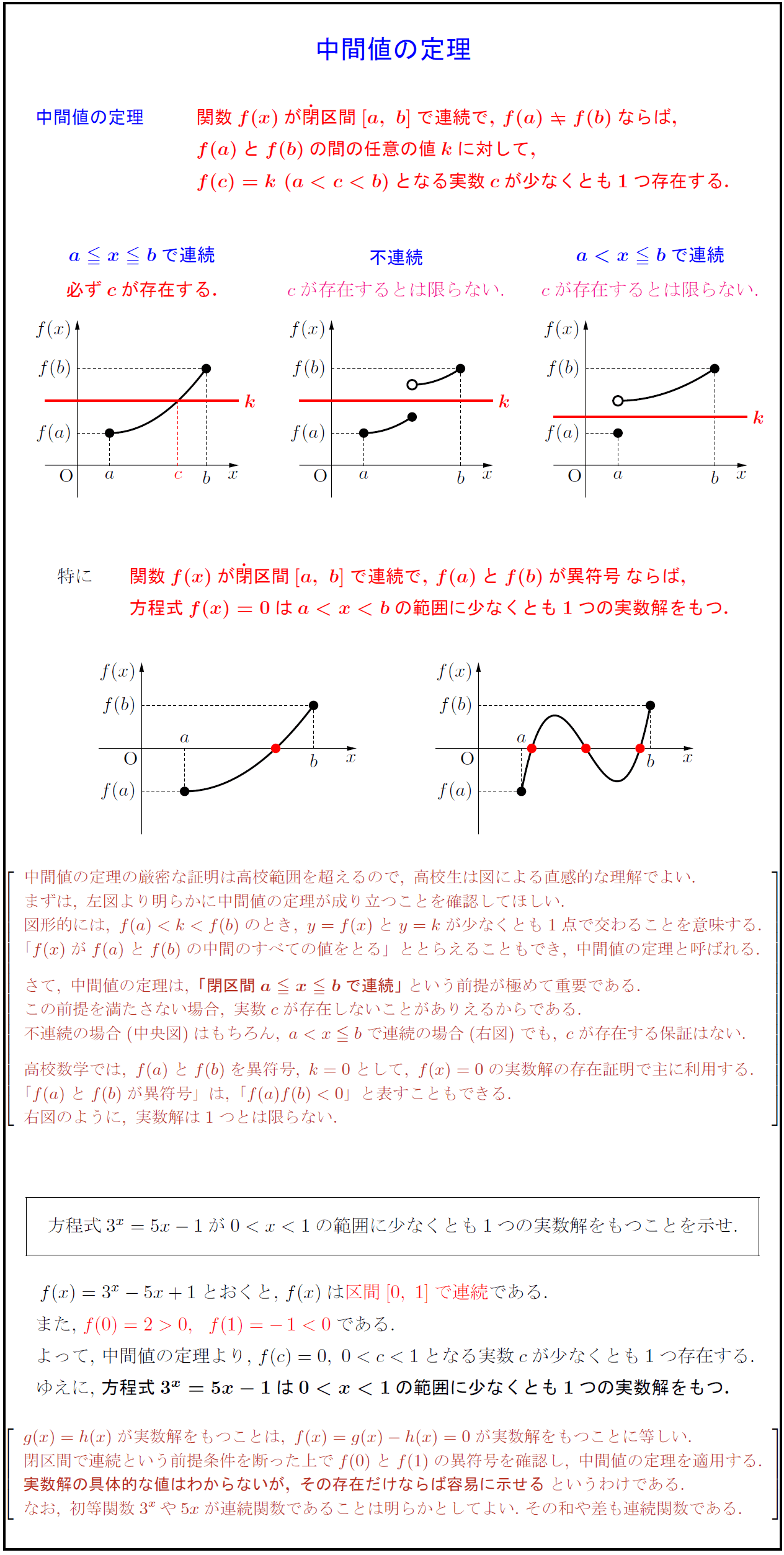



高校数学 中間値の定理 方程式の実数解の存在証明 受験の月




高校数学 関数f X の逆関数はf 1 X で表す 問題編 映像授業のtry It トライイット




どうして この解き方だとまずいのでしょうか Clear




高校数学 極値をもつ3次関数のグラフと最大 最小 映像授業のtry It トライイット




数学iiの問題です 添付写真の問題 宿題に出されたのですが 習いたてで解 Okwave




数学 For 大学受験 Su Twitter 解答 Lemmaの証明は読者の演習問題とする としたかったけど 余白があったので簡単に書いてます また 固有値lは固有値問題ax Lx X 0 を解けば容易に出てきます 詳しい解き方と固有ベクトルの求め方くらいは演習問題とさせて



大学数学の問題です 関数f X が次で定義されているとして 1 3の関 Yahoo 知恵袋




高校数学a 整数 F X が整数となる条件 F X が平方数となる条件 受験の月




高校数学 積分方程式 変数型 D Dx F T Dt F X の利用 受験の月



数学の問題 関数f X N 1 2 3 はf1 X Yahoo 知恵袋




極限計算の本質を解説してみた 大学受験数学の解き方



合成関数とは 微分 積分の公式や証明 問題の解き方 受験辞典




数学の質問なのですが 写真の問題の解き方が分かりません 解説お願い 数学 教えて Goo




微分不可能な関数の例は 微分可能性の直感的な理解




数i 絶対値のついた不等式の解き方 数学の偏差値を上げて合格を目指す




F 0 の意味がわかりません お願いします Clear




数学iiです 線を引いている部分が分かりません 解き方を詳しく教え 数学 教えて Goo




高校数学 微分の3本柱 積の微分法とその公式の証明 F X G X F X G X F X G X 受験の月




数学の下記問題の解き方を教えてください 講師に質問しても 人力検索はてな



数学の積分に関しての質問です 1 Xlogxを不定積分で解く際に 微分 Yahoo 知恵袋




高校数学 y F X の極値とグラフ 練習編 映像授業のtry It トライイット



高校2年数学iiです 三次方程式を 解け という問題の解き方が Yahoo 知恵袋
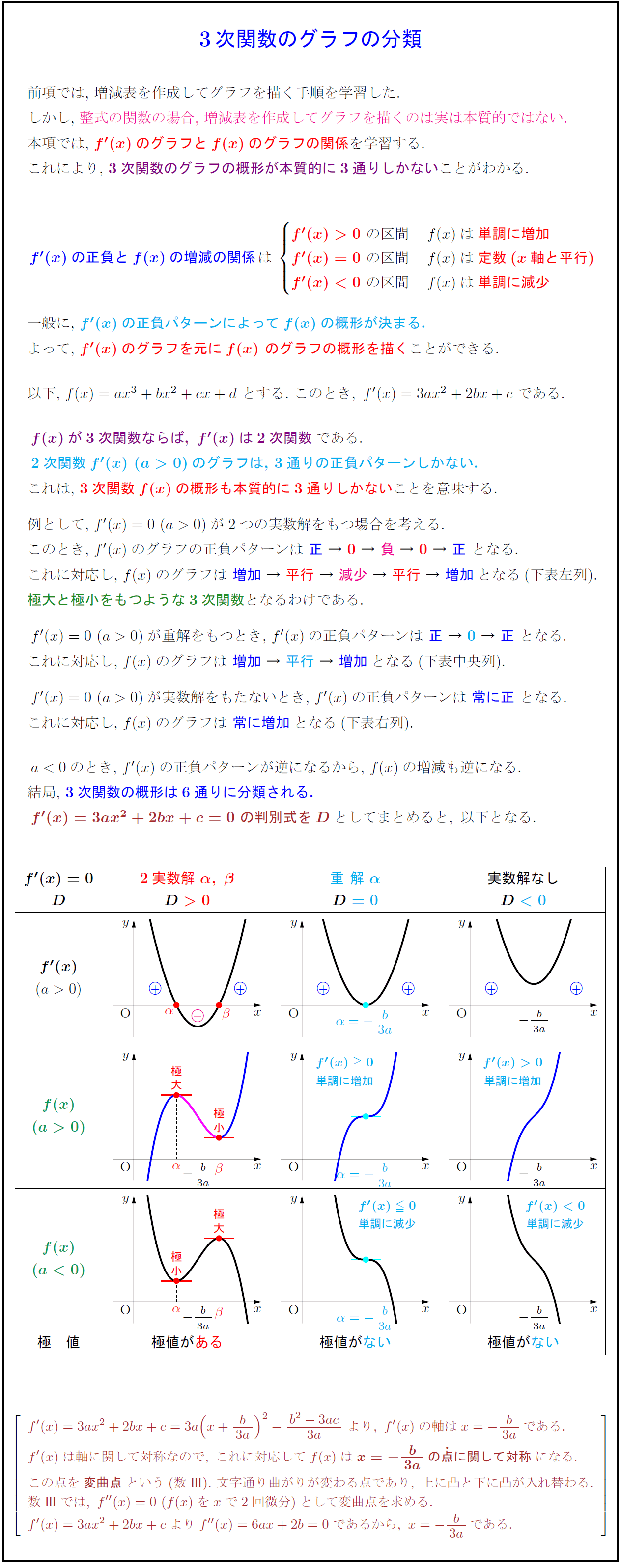



高校数学 3次関数のグラフの分類 F X のグラフとf X のグラフの関係 受験の月



高校数学の設問です 正解 Abcd 4122efghij Yahoo 知恵袋




2次関数 F X の意味 数学 定期テスト対策サイト




問題文の意味が分かりません 解き方も教えていただけるとなお嬉しいです Clear




微分可能な関数の極値を求めてみよう 2変数関数f X Y を中心に 身勝手な主張




関数方程式 基本の4パターン 数学の偏差値を上げて合格を目指す




はさみうちの原理による極限 大学受験数学の解き方




数学 F X G X となる範囲 すべての ある の違いを理解しておこう 数スタ




解き方を教えて頂けると助かります Clear




高校数学 関数方程式頻出4パターン 受験の月



0 件のコメント:
コメントを投稿